Úlohy: 121–140 / 140

34567
Přehled ročníků

121. Kolikrát je menší zlomek

Vypočtěte, kolikrát menší je 10 stotisícin než 5 desetisícin.
Řešení
Je menší 5krát.

122. Po sobě jdoucí čísla

Součet pěti po sobě jdoucích přirozených čísel je 555.

Vypočtěte, jaké je nejmenší z těchto čísel.
Řešení
Nejmenší číslo je 109.

123. Peníze v pokladničce

Karel má v pokladničce celkem 19 mincí, a to pouze desetikorunové a padesátikorunové mince. Celkem má v pokladničce naspořeno 830 Kč.

O každém z následujících tvrzení rozhodněte, jestli je pravdivé či nikoliv.
a)   V pokladničce chybí 170 Kč do tisíce.
b)   V pokladničce je méně desetikorun než padesátikorun.
c)   V pokladničce je o 13 padesátikorun více než desetikorun.
d)   V pokladničce je stejný počet desetikorun a padesátikorun.
e)   V pokladničce jsou desetikoruny a padesátikoruny v poměru 3 : 16 (v tomto pořadí).
Řešení
a)   0
b)   0
c)   0
d)   1
e)   0

124. Jablka v přepravce

Sadař nasbíral 294 kg jablek a rozdělil je do 42 přepravek.

Vypočtěte, kolik kg jablek bylo v jedné přepravce.
Řešení
V jedné přepravce bylo 7 kg jablek.

125. Objem krychlové nádoby

Nádoba tvaru krychle má bez víka povrch 320 centimetrů2.

Vypočítejte její objem v cm3.
Řešení
Objem nádoby je 512 cm3.

126. Povrch a objem krychle

Krychle má povrch 486 dm2.

Vypočtěte v dm3 objem této krychle.
Řešení
V = 729 dm3

127. Kolikrát větší

Vypočtěte, kolikrát větší je 6 setin než 24 desetitisícin.
Řešení
Je větší 25krát.

128. Dvě krabice

Krabice má tvar kvádru o rozměrech 3 cm, 4 cm a 5 cm.

Vypočítejte, kolikrát větší je objem druhé krabice s dvojnásobnými rozměry.
Řešení
Objem druhé krabice je 8krát větší.

129. Bakterie ve zkumavce

Bakterie ve zkumavce se dělí každou sekundu na dvě, přičemž každá nová má stejný objem jako původní. Přesně o půlnoci byla zkumavka plná.

Vypočítejte, kolik sekund před půlnocí byla zkumavka zaplněna do poloviny.
Řešení
Počet sekund před půlnocí, kdy byla zkumavka zaplněná do poloviny, bylo 1.

130. Vepsaná krychle

Do krychle k1 s délkou hrany a je vepsána koule krychle g. Do koule g je vepsána krychle k2.

Vypočtěte, kolik procent objemu krychle k1 tvoří objem krychle k2.
Řešení
Krychle k2 tvoří 19,25 % objemu krychle k1.

131. Akvárium

Akvárium ve tvaru kvádru má rozměry dna 6×3 dm a výšku 4 dm. Je naplněno vodou 5 cm pod okraj.

Na chov 1 rybičky je nutné mít 6 litrů vody.

Vypočtěte
a)   kolik nejvíce rybiček lze v akváriu chovat,
b)   kolik litrů vody zbylo v akváriu poté, se hladina vody snížila o 1 cm.
Řešení
a)   V akváriu lze chovat nejvíce 10 rybiček.
b)   V akváriu zbylo 61,20 litrů vody.

132. Rozvrh hodin v 1. A

Děti v 1. A mají v rozvrhu od pondělí do pátku každý den 4 vyučovací hodiny. V úterý mají ještě dvě hodiny odpoledního vyučování.

Vypočtěte, kolik vyučovacích hodin za týden mají děti v 1. A.
Řešení
Děti v 1. A mají za týden 22 vyučovacích hodin.

133. Poustevník a krkavci

Poustevník měl 12 krkavců. Všichni, kromě 5 uletěli.

Vypočtěte, kolik krkavců poustevníkovi zbylo.
Řešení
Poustevníkovi zbylo 5 krkavců.

134. Pletení košíků

Košíkář plete košíky od pondělí do neděle. V pondělí upletl 7 košíků a každý další den o jeden více než předchozí den.

Kolikrát více košíků upletl košíkář za celý týden ve srovnání s pondělkem.
Řešení
Za celý týden upletl košíkář 10krát více košíků než v pondělí.

135. Sčítání a odčítání čísel

Vypočítejte příklady:
a)    0 + 3 – 2 + 0 – 1 + 3 + 0 – 2 + 4 – 0 =
b)    4 + 6 - 2 + 1 - 5 - 2 + 3 =
c)    7 - 3 + 2 - 1 + 5 - 6 + 3 =
d)    2 + 3 + 4 - 8 + 1 + 5 - 3 + 4 =
Řešení
a)   5
b)   5
c)   7
d)   7

136. Banány a pomeranče

Šimon má 10 banánů, Adam má 25 pomerančů.

Vpočtěte, kolik mají dohromady kusů ovoce?
Řešení
Dohromady mají 30 kusů ovoce.

137. Vnitřní úhly v trojúhelníku

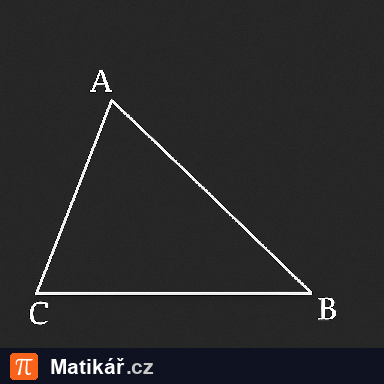
V trojúhelníku ABC je velikost vnitřního úhlu \( \beta \) o 10 stupňů větší než velikost úhlu \( \alpha \) a velikost úhlu \( \gamma \) je 3× větší než velikost úhlu \( \beta \).

Určete velikost úhlů:
a)   \( \alpha \)
b)   \( \beta \)
c)   \( \gamma \)
Řešení
a)   Velikost úhlu \( \alpha \) je 28 °,
b)   velikost úhlu \( \beta \) je 38 °,
c)   velikost úhlu \( \gamma \) je 114 °.

138. Uspořené peníze

Honza uspořil 72 korun. Pepík uspořil o 9 korun více než Honza.

Vypočtěte, kolik korun uspořil Pepík.
Řešení
Pepík uspořil 81 korun.

139. Sázené růže

Zahradník sázel růže. Do každého řádku zasadil 13 růží. Po raním mrazíku jí mnoho sazenic uhynulo.

V 1 řádku uhynulo 5 růží.

V 2 řádku uhynulo o 2 růže více než v 1 řádku.

Ve 3 řádku uhynulo o 3 růže méně než v 1 řádku.

Ve 4 řádku uhynulo o 1 růži víc než ve 3 řádku.

Vypočtěte, kolik růží musel zahradník doplnit, aby byl ve všech řádcích opět po 13 růžích.
Řešení
Zahradník musel doplnit 17 růží.

140. Slepice a zrní

15 slepic by sezobalo rozsypané zrní od 6 hodin do 16 hodin. V 9 hodin však babička přinesla 6 slepic, které dokoupila od sousedky.

Vypočtěte, v kolik hodin bylo zrní sezobáno.
Řešení
Zrní bylo sezobáno ve 14 hodin.
 
34567