Úlohy: 1–20 / 190

12345
Přehled ročníků

1. Mocniny s přirozeným mocnitelem

Upravte jako mocniny prvočísel:
a)   
b)   
c)   
d)   
e)   
f)   
Řešení
a)   
b)   
c)   
d)   
e)   
f)   
Matematická úloha – Mocniny s přirozeným mocnitelem

2. Mocniny s přirozeným mocnitelem

Upravte jako mocniny prvočísel:
a)   
b)   
c)   
d)   
e)   
f)   
Řešení
a)   
b)   
c)   
d)   
e)   
f)   
Matematická úloha – Mocniny s přirozeným mocnitelem

3. Mocniny s přirozeným mocnitelem

Upravte jako mocniny prvočísel:
a)   
b)   
c)   
d)   
e)   
f)   
Řešení
a)   
b)   
c)   
d)   
e)   
f)   
Matematická úloha – Mocniny s přirozeným mocnitelem

4. Goniometrické rovnice 2

Vyřešte goniometrické rovnice:
a)   \[ \sin x = \frac{1}{2} \]
b)   \[ \cos x = -\frac{\sqrt{3}}{2} \]
c)   \[ \tan x = 1 \]
d)   \[ \sin 2x = 0 \]
e)   \[ 2\cos^2 x - 1 = 0 \]
f)   \[ \sin^2 x = \frac{1}{4} \]
Řešení
a)   \[ x = \frac{\pi}{6} + 2k\pi, \, x = \frac{5\pi}{6} + 2k\pi \]
b)   \[ x = \frac{5\pi}{6} + 2k\pi, \, x = \frac{7\pi}{6} + 2k\pi \]
c)   \[ x = \frac{\pi}{4} + k\pi \]
d)   \[ x = \frac{k\pi}{2} \]
e)   \[ x = \frac{\pi}{4} + 2k\pi, \, x = \frac{3\pi}{4} + 2k\pi, \,\]\[x = \frac{5\pi}{4} + 2k\pi, \, x = \frac{7\pi}{4} + 2k\pi \]
f)   \[ x = \frac{\pi}{6} + 2k\pi, \, x = \frac{5\pi}{6} + 2k\pi, \,\]\[x = \frac{7\pi}{6} + 2k\pi, \, x = \frac{11\pi}{6} + 2k\pi \]
Matematická úloha – Goniometrické rovnice 2

5. Definiční obor funkcí 2

Určete definiční obory \( D_f \) následujících funkcí:
a)   \[ f(x) = \frac{1}{x^2 - 4} \]
b)   \[ g(x) = \sqrt{x^2 - 9} \]
c)   \[ h(x) = \ln(2x - 1) \]
d)   \[ k(x) = \frac{\sqrt{5 - x}}{x + 3} \]
e)   \[ m(x) = \sqrt{x + \ln(x)} \]
f)   \[ n(x) = \frac{\ln(x - 1)}{x^2 - 4x + 3} \]
Řešení
a)   \( D_f = (-\infty, -2) \cup (-2, 2) \cup (2, \infty) \)
b)   \( D_g = (-\infty, -3\rangle \cup \langle 3, \infty) \)
c)   \( D_h = \langle \frac{1}{2}, \infty) \)
d)   \( D_k = (-\infty, -3) \cup (-3, 5\rangle \)
e)   \( D_m = (0, \infty) \)
f)   \( D_f = (1, 3) \cup (3, \infty) \)
Matematická úloha – Definiční obor funkcí 2

6. Hodnost matic 2

Určete hodnost následujících matic:
a)   \[ A = \begin{pmatrix} 2 & 4 & 6 \\ 1 & 2 & 3 \\ 3 & 6 & 9 \end{pmatrix} \]
b)   \[ B = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 10 \end{pmatrix} \]
c)   \[ C = \begin{pmatrix} 2 & -1 & 3 \\ 1 & 0 & -2 \\ 4 & -3 & 6 \end{pmatrix} \]
d)   \[ D = \begin{pmatrix} 1 & 2 & 3 \\ 0 & 0 & 0 \\ 4 & 5 & 6 \end{pmatrix} \]
e)   \[ E = \begin{pmatrix} 3 & 6 & 9 \\ 1 & 2 & 3 \\ 0 & 0 & 0 \end{pmatrix} \]
f)   \[ F = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 3 \end{pmatrix} \]
Řešení
a)   \( \text{hodnost}(A) = 1 \)
b)   \( \text{hodnost}(B) = 3 \)
c)   \( \text{hodnost}(C) = 3 \)
d)   \( \text{hodnost}(D) = 2 \)
e)   \( \text{hodnost}(E) = 1 \)
f)   \( \text{hodnost}(F) = 3 \)
Matematická úloha – Hodnost matic 2

7. Determinant matic

Určete determinant matic převodem na trojúhelníkový tvar:
a)   \[ A = \begin{pmatrix} 2 & -1 & 3 \\ 1 & 0 & -2 \\ 4 & -3 & 6 \end{pmatrix} \]
b)   \[ B = \begin{pmatrix} 3 & 1 & -2 \\ 0 & 4 & 1 \\ 2 & -3 & 5 \end{pmatrix} \]
c)   \[ C = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 10 \end{pmatrix} \]
d)   \[ D = \begin{pmatrix} 2 & 3 & 1 \\ 1 & 5 & -1 \\ 4 & 7 & 3 \end{pmatrix} \]
e)   \[ E = \begin{pmatrix} 6 & 2 & -1 \\ 0 & 5 & 3 \\ 1 & 4 & 2 \end{pmatrix} \]
f)   \[ F = \begin{pmatrix} 1 & 0 & 2 \\ 3 & 4 & -1 \\ 5 & -2 & 0 \end{pmatrix} \]
Řešení
a)   \( \text{det}(A) = 7 \)
b)   \( \text{det}(B) = 63 \)
c)   \( \text{det}(C) = -3 \)
d)   \( \text{det}(D) = 10 \)
e)   \( \text{det}(E) = 12 \)
f)   \( \text{det}(F) = -54 \)
Matematická úloha – Determinant matic

8. Parametrické a obecné rovnice

Jsou dány parametrické rovnice.

Převeďte rovnice na obecný tvar:
a)   \( x = 2t + 1, \quad y = 3t - 4 \)
b)   \( x = t - 3, \quad y = 4t + 2 \)
c)   \( x = 5t + 2, \quad y = 6t - 1 \)
d)   \( x = -2t + 4, \quad y = t - 5 \)
e)   \( x = 3t + 7, \quad y = -t + 2 \)
f)   \( x = 4t - 6, \quad y = 2t + 8 \)
Řešení
a)   \( 3x - 2y - 11 = 0 \)
b)   \( 4x - y + 14 = 0 \)
c)   \( 6x - 5y - 17 = 0 \)
d)   \( x + 2y + 6 = 0 \)
e)   \( x + 3y - 13 = 0 \)
f)   \( 2x - 4y + 44 = 0 \)
Matematická úloha – Parametrické a obecné rovnice

9. Obecné a parametrické rovnice

Jsou zadané obecné rovnice přímek v rovině.

Převeďte rovnice na parametrický tvar:
a)   \( 2x + 3y - 6 = 0 \)
b)   \( x - 4y + 8 = 0 \)
c)   \( 3x + 2y - 12 = 0 \)
d)   \( 5x - y - 15 = 0 \)
e)   \( x + y - 7 = 0 \)
f)   \( 4x - 3y + 9 = 0 \)
Řešení
a)   \(x = t, \quad y = \frac{6 - 2t}{3}\)
b)   \(x = t, \quad y = \frac{t + 8}{4}\)
c)   \(x = t, \quad y = \frac{12 - 3t}{2}\)
d)   \(x = t, \quad y = 5t - 15\)
e)   \(x = t, \quad y = 7 - t\)
f)   \(x = t, \quad y = \frac{4t + 9}{3}\)
Matematická úloha – Obecné a parametrické rovnice

10. Kvadratické nerovnice

Vyřešte kvadratické nerovnice:
a)   \(x^2 - 4x - 5 > 0\)
b)   \(x^2 + 3x - 10 \leq 0\)
c)   \(2x^2 - 8x \geq 0\)
d)   \(-x^2 + 5x + 14 < 0\)
e)   \(x^2 - 6x + 9 > 0\)
f)   \(2x^2 - 12x + 16 \leq 0\)
Řešení
a)   \((- \infty, -1) \cup (5, \infty)\)
b)   \(\langle -5, 2 \rangle\)
c)   \((- \infty, 0 \rangle \cup \langle 4, \infty)\)
d)   \(x \in (-\infty, -2) \cup (7, \infty)\)
e)   \((- \infty, 3) \cup (3, \infty)\)
f)   \(\langle 2, 4 \rangle\)
Matematická úloha – Kvadratické nerovnice

11. Uložené peníze

Petr si založil spořicí účet, na který vložil 50 000 Kč. Banka nabízí roční úrokovou sazbu 3 % s ročním připisováním úroků (složené úročení). Peníze nechá na účtu 5 let.

Jakou částku bude mít Petr na účtu, pokud nebude vkládat ani vybírat peníze?
Řešení
Po 5 letech bude mít Petr na účtu přibližně 57 963,70 Kč.
Matematická úloha – Uložené peníze

12. Goniometrické rovnice 1

Vyřešte goniometrické rovnice:
a)   \[\sin x = \frac{1}{2}\]
b)   \[\cos x = -\frac{\sqrt{2}}{2}\]
c)   \[\tan x = \sqrt{3}\]
d)   \[\sin^2 x = \frac{3}{4}\]
e)   \[\cos 2x = 0\]
f)   \[\tan^2 x = 3\]
Řešení
a)   \[x = \frac{\pi}{6} + 2k\pi \lor x = \frac{5\pi}{6} + 2k\pi, k \in \mathbb{Z}\]
b)   \[x = \frac{3\pi}{4} + 2k\pi \lor x = \frac{5\pi}{4} + 2k\pi, k \in \mathbb{Z}\]
c)   \[x = \frac{\pi}{3} + k\pi, k \in \mathbb{Z}\]
d)   \[x = \frac{\pi}{3} + 2k\pi \lor x = \frac{2\pi}{3} + 2k\pi \lor x = \frac{4\pi}{3} + 2k\pi \lor x = \frac{5\pi}{3} + 2k\pi, k \in \mathbb{Z}\]
e)   \[x = \frac{\pi}{4} + \frac{k\pi}{2}, k \in \mathbb{Z}\]
f)   \[x = \frac{\pi}{3} + k\pi \lor x = -\frac{\pi}{3} + k\pi, k \in \mathbb{Z}\]
Matematická úloha – Goniometrické rovnice 1

13. Koupě auta

Petr si chce za dva roky koupit nové auto. Ví, že cena auta bude 600 000 Kč. Plánuje si peníze odkládat na spořicí účet s ročním úrokem 4 %, který se připisuje na konci každého roku.

Vypočítejte, kolik musí Petr vložit na tento účet dnes, aby měl za dva roky dostatek peněz na nákup auta.
Řešení
Petr musí vložit na účet částku 554 705 Kč.
Matematická úloha – Koupě auta

14. Plnění zásobníku vodou

Zásobník na vodu má tvar válce o poloměru základny 50 cm a výšce ( frac{3}{pi} , ext{m} ). Aktuálně je naplněn ze 40 %. Do zásobníku začala téct voda rychlostí 1 litr za 2 sekundy.

Vypočítejte, za jak dlouho bude zásobník naplněn z 90 %. (Zapište v minutách a sekundách.)
Řešení
Zásobník bude naplněn z 90 % za 12 minut 30 sekund.
Matematická úloha – Plnění zásobníku vodou

15. Úhly v trojúhelníku

Určete velikosti všech úhlů v trojúhelníku, který je zadán souřadnicemi tří bodů. Výsledky zapište ve stupních na dvě desetinná místa.
a)   \( A(1, 2), \quad B(4, 6), \quad C(7, 2). \)
b)   \( A(-2, 1), \quad B(3, 4), \quad C(1, -3). \)
c)   \( A(2, 3), \quad B(6, 3), \quad C(6, 7). \)
d)   \( A(1, 1), \quad B(4, 5), \quad C(7, 2). \)
Řešení
a)   \[ \alpha \approx 53.13^\circ, \quad \beta \approx 73.74^\circ, \quad \gamma \approx 53.13^\circ.\]
b)   \[ \alpha \approx 79.1^\circ, \quad \beta \approx 50.9^\circ, \quad \gamma \approx 50^\circ. \]
c)   \[ \alpha = 45^\circ, \quad \beta = 45^\circ, \quad \gamma = 90^\circ. \]
d)   \[ \alpha \approx 48.6^\circ, \quad \beta \approx 60^\circ, \quad \gamma \approx 71.4^\circ. \]
Matematická úloha – Úhly v trojúhelníku

16. Průsečík dvou rovin

Najděte průsečík rovin:
a)   \[ \text{Rovina } \rho_1 \text{: } x = 2 + s, \quad y = s + t, \quad z = 3 + t, \quad s, t \in \mathbb{R}.\] \[ \text{Rovina } \rho_2 \text{: } x = 4 + u, \quad y = 2u - v, \quad z = 5 - v, \quad u, v \in \mathbb{R}. \]
b)   \[ \text{Rovina } \rho_1 \text{: } x = s, \quad y = 2 + s + t, \quad z = 3 + t, \quad s, t \in \mathbb{R}. \] \[ \text{Rovina } \rho_2 \text{: } x = u + v, \quad y = 4 - u, \quad z = 6 + v, \quad u, v \in \mathbb{R}. \]
c)   \[ \text{Rovina } \rho_1 \text{: } x = 3 + s, \quad y = -s, \quad z = 2 - t, \quad s, t \in \mathbb{R}. \] \[ \text{Rovina } \rho_2 \text{: } x = 3 + 2u - v, \quad y = u - 2v, \quad z = 2 + u + v, \quad u, v \in \mathbb{R}. \]
d)   \[ \text{Rovina } \rho_1 \text{: } x = 1 + s, \quad y = 1 + t, \quad z = 1 + t, \quad s, t \in \mathbb{R}.\] \[ \text{Rovina } \rho_2 \text{: } x = 2 + u, \quad y = 2 - v, \quad z = 2 - v, \quad u, v \in \mathbb{R}. \]
Řešení
a)   \[ x = 4, \quad y = 8 - v, \quad z = 5 - v, \quad v \in \mathbb{R}. \]
b)   \[ x = -\frac{1}{2} + v, \quad y = \frac{9}{2} + v, \quad z = 6 + v, \quad v \in \mathbb{R}. \]
c)   \[ x = 3 + v, \quad y = -v, \quad z = 2 + 2v, \quad v \in \mathbb{R}. \]
d)   \[ x = 1 + v, \quad y = 2 - v, \quad z = 2 - v, \quad v \in \mathbb{R}. \]
Matematická úloha – Průsečík dvou rovin

17. Světelné efekty ve městě

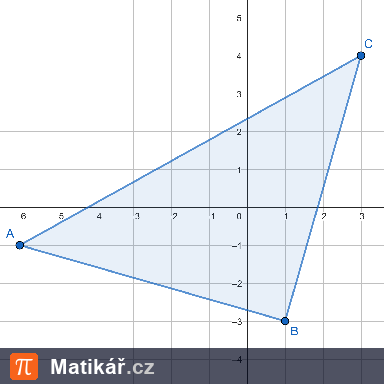
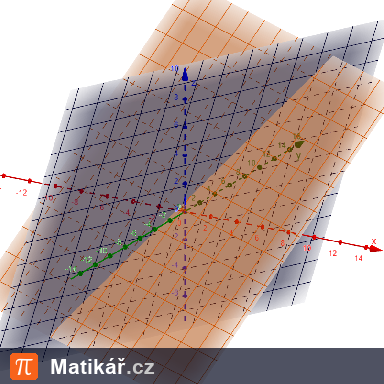
Ve městě se plánuje oslavná událost, na kterou organizátoři připravili speciální světelné show. K dispozici mají 4 různé barvy světel: červenou, modrou, zelenou a žlutou. Každou barvu mohou použít vícekrát a pořadí barev při show je důležité.

Vypočítejte, kolik různých sekvencí světel o délce 5 mohou organizátoři vytvořit.
Řešení
Organizátoři mohou vytvořit 1 024 různých sekvencí světel.
Matematická úloha – Světelné efekty ve městě

18. Limity funkcí

Pomocí l'Hospitalova pravidla vypočítejte limity funkcí:
a)   \[\lim_{x \to \infty} \frac{x}{e^x}\]
b)   \[\lim_{x \to 0^+} \frac{\ln(x)}{\frac{1}{x}}\]
c)   \[\lim_{x \to 0} \frac{\sin(x)}{x^2}\]
d)   \[\lim_{x \to 1} \frac{x^2 - 1}{x - 1}\]
e)   \[\lim_{x \to \infty} \frac{\ln(x)}{\sqrt{x}}\]
f)   \[\lim_{x \to 0} \frac{\tan(x)}{x}\]
Řešení
a)   0
b)   0
c)   0
d)   2
e)   0
f)   1
Matematická úloha – Limity funkcí

19. Derivace funkcí

Vypočítejte derivace následujících funkcí:
a)   \[ f(x) = x^2 \cdot e^x \]
b)   \[ g(x) = \frac{x^2 + 3}{x - 1} \]
c)   \[ h(x) = \sin(x) \cdot \cos(x) \]
d)   \[ k(x) = \sqrt{x^2 + 1} \]
e)   \[ m(x) = e^{\sin(x)} \]
f)   \[ p(x) = \ln(x^2 + 1) \]
Řešení
a)   \[ f'(x) = e^x (2x + x^2) \]
b)   \[g'(x) = \frac{x^2 - 2x - 3}{(x - 1)^2}\]
c)   \[h'(x) = \cos(2x)\]
d)   \[k'(x) = \frac{x}{\sqrt{x^2 + 1}}\]
e)   \[m'(x) = e^{\sin(x)} \cos(x)\]
f)   \[p'(x) = \frac{2x}{x^2 + 1}\]
Matematická úloha – Derivace funkcí

20. Sarrusovo pravidlo

Vypočítejte determinant pomocí Sarrusova pravidla:
a)   \[ \begin{vmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{vmatrix} \]
b)   \[ \begin{vmatrix} 2 & 1 & 3 \\ 1 & 4 & 2 \\3 & 5 & 6 \end{vmatrix}\]
c)   \[ \begin{vmatrix} 3 & 0 & 1 \\ 2 & 4 & 5 \\ 1 & 3 & 2 \end{vmatrix}\]
d)   \[ \begin{vmatrix}1 & 3 & 5 \\2 & 1 & 4 \\3 & 2 & 1\end{vmatrix}\]
e)   \[ \begin{vmatrix} 5 & 2 & 0 \\ 1 & 3 & 2 \\ 4 & 1 & 3\end{vmatrix}\]
f)   \[\begin{vmatrix}1 & 2 & 3 \\ 0 & 1 & 4 \\ 5 & 6 & 0 \end{vmatrix}\]
Řešení
a)   \( 0 \)
b)   \( 7 \)
c)   \( -19 \)
d)   \( 28 \)
e)   \( 45 \)
f)   \( 1 \)
Matematická úloha – Sarrusovo pravidlo
 
12345