Úlohy: 41–60 / 190

12345
Přehled ročníků

41. Kvadratická funkce zadaná třemi body

V kartézské soustavě souřadnic jsou dány body.

Určete předpis kvadratické funkce, která prochází body:
a)   
b)   
c)   
d)   
e)   
f)   
Řešení
a)   
b)   
c)   nemá řešení
d)   
e)   nekonečně mnoho řešení
f)   
g)   
Matematická úloha – Kvadratická funkce zadaná třemi body

42. Budova ve tvaru písmene H

Budova ve tvaru písmene H se skládá ze 3 částí. Dvě stejné části mají následující rozměry, výška 805 cm, šířka 525 cm, délka je 15 m. Třetí část ve tvaru krychle má šířku 7 m.

Vypočítejte, jaký je celkový objem budovy v metrech krychlových. (Zaokrouhlete na dvě desetinná místa.)
Řešení
Celkový objem budovy je 1 611,63 m³.
Matematická úloha – Budova ve tvaru písmene H

43. Úhlopříčky v rovnoběžníku

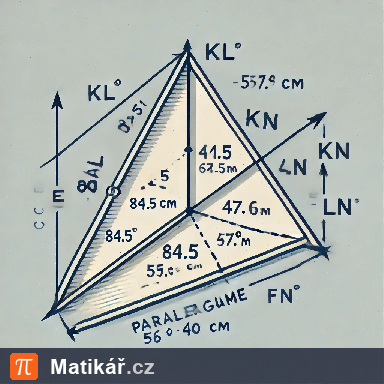
Je dán rovnoběžník KLMN, ve kterém známe velikosti stran \( a = |KL| = 84,5 \, \mathrm{cm} \), \( d = |KN| = 47,8 \, \mathrm{cm} \) a velikost úhlu \( \alpha = \angle NKL = 56^\circ 40' \).

Vypočítejte v centimetrech velikost
a)   úhlopříčky \( e = |KM| \),
b)   úhlopříčky \( f = |LN| \).
Řešení
a)   Úhlopříčka e je dlouhá 99,86 cm.
b)   Úhlopříčka f je dlouhá 166,52 cm.
Matematická úloha – Úhlopříčky v rovnoběžníku

44. Rovnice kružnice

Napište rovnici kružnice, která prochází body Q[3; 5], R[2; 6] a má střed na přímce .
Řešení
Matematická úloha – Rovnice kružnice

45. Test na základní škole

V základní škole psali test, v němž každý žák mohl získat nejvýše 15 bodů. Letos byl průměrný bodový zisk žáků zaokrouhlený na desetiny roven 10,40. Libor si po testu uvědomil, že některé otázky si špatně přečetl a odpověděl na něco jiného. Mohl tak mít o 4 body více a průměrný bodový zisk zaokrouhlený na desetiny by se tím zvýšil na 10,60.

Vypočítejte, kolik
a)   nejméně dětí mohlo psát test,
b)   nejvíc dětí mohlo psát test.
Řešení
a)   Minimální počet dětí, které mohly psát test, je 14.
b)   Maximální počet dětí, které mohly soutěžit, je 40.
Matematická úloha – Test na základní škole

46. Trosečník na ostrově

Trosečník přišel na pustý ostrov se 4 obilnými zrnky. Z jednoho zrnka získal 10 zrnek a na chléb potřeboval 1 kg obilí a 1 zrnko má hmotnost asi 0,20 g? (Předpokládejme jednu úrodu za rok.)

Vypočítejte, kolik let trosečníkovi trvalo, než si vypěstoval dost obilí na chléb.
Řešení
Trosečníkovi trvalo 4 roky, než si vypěstoval dost obilí na chléb.
Matematická úloha – Trosečník na ostrově

47. Třídička brambor

Kvůli velké úrodě brambor letos přikoupili na statku ke staré třídičce novou, výkonnější. Nyní pracují oba stroje současně, a proto je denní sklizeň zpracována za 12 hodin. Kdyby pracoval pouze starý stroj, potřeboval by ke zpracování denní sklizně o 10 hodin více než samotný nový stroj.

Vypočítejte, jak dlouho by to staré třídičce trvalo. Zapište v hodinách a minutách.
Řešení
Staré třídičce by to trvalo 30 hodin.
Matematická úloha – Třídička brambor

48. Násobení zlomků s neznámou

Když sečteme zlomky a dostaneme stejný výsledek, jako když je vynásobíme.

Vypočítejte hodnotu x.
Řešení
Řešením je číslo 7.
Matematická úloha – Násobení zlomků s neznámou

49. Tisk papíru

Tiskárna vytiskne 5 stránek za p sekund.

Vypočítejte, kolik stránek vytiskne tiskárna za p minut.
Řešení
Za p minut vytiskne tiskárna 300 stránek.
Matematická úloha – Tisk papíru

50. Ukládání knih do knihovny

Lucie má 5 různých knih, z nichž 2 určité knihy chtějí být vedle sebe na polici.

Vypočítejte, kolika různými způsoby může Lucie uspořádat všech 5 knih na polici s tímto požadavkem.
Řešení
Lucie může naskládat knihy do knihovny 48 možnými způsoby.
Matematická úloha – Ukládání knih do knihovny

51. Výběr filmů

Evžen si stáhl 5 různých filmů ale má čas si pustit pouze 3, je jedno v jakém pořadí.

Vypočítejte, kolika různými způsoby může Evžen vybrat filmy, které si pustí.
Řešení
Evžen může vybrat filmy 10 různými způsoby.
Matematická úloha – Výběr filmů

52. Definiční obor funkcí 1

Určete definiční obory \( D_f \) následujících funkcí:
a)   \[ f(x) = \frac{1}{x - 2} \]
b)   \[ g(x) = \sqrt{5 - x} \]
c)   \[ h(x) = \ln(x + 3) \]
d)   \[ k(x) = \frac{\sqrt{x + 1}}{x - 4} \]
e)   \[ m(x) = \sqrt{3x + 9} \]
f)   \[ n(x) = \frac{\ln(x)}{x^2 - 1} \]
Řešení
a)   \[ D_f = (-\infty, 2) \cup (2, \infty).\]
b)   \[ D_g = (-\infty, 5\rangle.\]
c)   \[ D_h = (-3, \infty).\]
d)   \[ D_k = \langle -1, 4) \cup (4, \infty).\]
e)   \[ D_m = \langle -3, \infty).\]
f)   \[ D_n = (0, 1) \cup (1, \infty).\]
Matematická úloha – Definiční obor funkcí 1

53. Cyklistická etapa

Tři cyklisté se absolvovali etapu po stejné trase. První cyklista jel průměrně o 6 kilometrů za hodinu rychleji než druhý a dojel do cíle o hodinu dříve. Naopak třetí cyklista jel průměrně o 6 kilometrů za hodinu pomaleji než druhý a dojel tak do cíle o 2 hodiny později.

Určete v kilometrech délku trasy.
Řešení
Trasa byla dlouhá 72 kilometrů.
Matematická úloha – Cyklistická etapa

54. Složení volejbalového týmu

U hřiště stojí 10 mužů a 8 žen.

Určete, kolika způsoby lze vybrat volejbalový tým (který má šest členů), s podmínkou, že:
a)   tým bude obsahovat právě dvě ženy,
b)   maximálně dvě ženy.
Řešení
a)   5 880 možností
b)   8 106 možností
Matematická úloha – Složení volejbalového týmu

55. Počet ťuknutí při přípitku

Na oslavě se sešlo 15 hostů. Při přípitku si každý s každým ťukl sklenicí právě jednou.

Vypočítejte, kolik zaznělo ťuknutí.
Řešení
Při přípitku zaznělo 105 ťuknutí.
Matematická úloha – Počet ťuknutí při přípitku

56. Vzdálenosti bodů

Jsou dány dvojice bodů v rovině.

Určete vzdálenost bodů v každé dvojici.
a)   A[-4;3], B[4;-3]
b)   C[-2;1], D[2;10]
c)   E[2;-1], F[-5;1]
d)   G[4;-3], H[-5;5]
Řešení
a)   10
b)    sqrt(97)
c)    sqrt(53)
d)    sqrt(145)
Matematická úloha – Vzdálenosti bodů

57. Úhly v devítiúhelníku

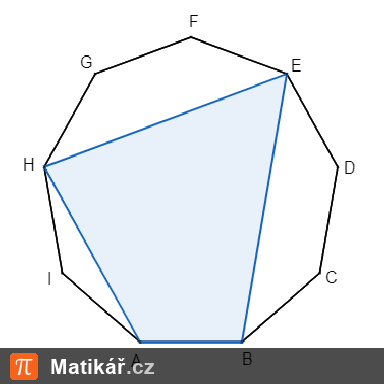
Je dán pravidelný devítiúhelník ABCDEFGHI.

Vypočítejte všechny vnitřní úhly čtyřúhelníku ABEH.
Řešení
Matematická úloha – Úhly v devítiúhelníku

58. Průnik koule a roviny

Určete v cm2 obsah kruhu, který je průnikem koule K(O; 10 cm) a roviny, která je vzdálená od bodu O 6 cm. (Zaokrouhlete na dvě desetinná místa.)

Řešení
Obsah kruhu je 25,13 cm2.

59. Vystřižené rovnoramenné trojúhelníky

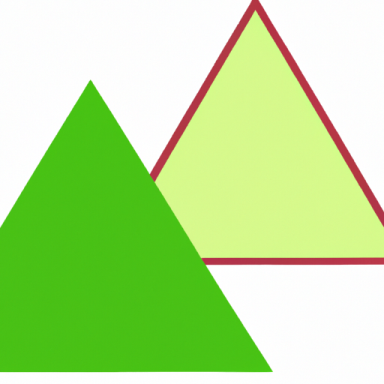
Jsou dány dva shodné rovnoramenné trojúhelníky, z nichž každý má obvod 100 cm. Nejprve z těchto trojúhelníků složíme rovnoběžník tak, že je k sobě přiložíme rameny. Poté z nich složíme kosočtverec tak, že je k sobě přiložíme základnami. Rovnoběžník má o 4 cm kratší obvod než kosočtverec.

Vypočítejte délky stran trojúhelníků.
Řešení
Základna má délku 32 cm, rameno má délku 34 cm.
Matematická úloha – Vystřižené rovnoramenné trojúhelníky

60. Plnící linky v mlékárně

V mlékárně mají dvě linky pro plnění krabic mléka. Nová linka je o 50 % rychlejší, než stará linka. Když pracují obě linky současně, naplní běžné denní množství krabic mléka o 6 hodin dříve, než když pracovala pouze stará linka.

Vypočítejte, za jak dlouho naplní denní množství krabic mléka, bude-li pracovat:
a)   pouze stará linka,
b)   pouze nová linka,
c)   obě linky současně.
Řešení
a)   Bude-li pracovat pouze stará linka, naplní denní množství krabic za 10 hodin a 0 minut.
b)   Bude-li pracovat pouze nová linka, naplní denní množství krabic za 6 hodin a 40 minut.
c)   Budou-li pracovat obě linky současně, naplní denní množství krabic za 4 hodin a 0 minut.
Matematická úloha – Plnící linky v mlékárně
 
12345