Úlohy: 81–100 / 127

34567
Přehled ročníků

81. Červené a bílé kuličky

Máme 15 červených a 5 bílých kuliček.

Vypočítejte v procentech, jaká je pravděpodobnost, že první vytažená kulička bude bílá.
Řešení
Pravděpodobnost, že první vytažená kulička bude bílá, je 25 %.
Matematická úloha – Červené a bílé kuličky

82. Obvod trojúhelníku ABC

Je dán trojúhelník ABC. Délka strany a je rovna dvou třetinám strany c. Délka strany c je rovna třem pětinám délky strany b. Délka strany b je 15 cm.

Vypočítejte obvod trojúhelníku ABC.
Řešení
Obvod trojúhelníku ABC je 50 cm.
Matematická úloha – Obvod trojúhelníku ABC

83. Pizza v krabicích

Na stole jsou dvě krabice pizzy stejné velikosti. V jedné krabici je pizzy a ve druhé pizzy. Potom kuchař rozdělí obě pizzy na dílky tak, že jeden dílek je pizzy.

Určete, kolik kousků pizzy bylo v krabicích.
Řešení
V krabicích bylo 10 kousků pizzy.
Matematická úloha – Pizza v krabicích

84. Doplnění poměru

Doplň místo x takové číslo, aby platila rovnost.
a)   \( \frac{5}{6} = \frac{15}{x} \)
b)   \( \frac{3}{2} + 1 = \frac{x}{10} \)
Řešení
a)   18
b)   25
Matematická úloha – Doplnění poměru

85. Hrušky

Filip má 8 hrušek. Filip má o 5 hrušek méně než Radek.

Vypočítejte, kolik hrušek mě Radek.
Řešení
Radek má 13 hrušek.
Matematická úloha – Hrušky

86. Části čísel

Vypočítejte, o kolik jsou dvě sedminy z 420 menší než tři osminy z 960.
Řešení
Rozdíl je 240.
Matematická úloha – Části čísel

87. Střední příčka lichoběžníku

Obsah lichoběžníku je 111,80 cm2 a jeho výška 6,50 cm.

Vypočítejte v cm délku střední příčky lichoběžníku.
Řešení
Velikost střední příčky lichoběžníku je 17,20 cm.
Matematická úloha – Střední příčka lichoběžníku

88. Cyklistický závod

Po 30 km je cyklista v jedné pětině závodu.

Vypočtěte, jak dlouhý je celý závod.
Řešení
Závod je dlouhý 150 km.
Matematická úloha – Cyklistický závod

89. Průměrná denní teplota

Teplota během dne byla pravidelně měřena. Ráno byla teplota -3 °C. Ve poledne teplota vystoupila na 12 °C. Po setmění teplota opět klesla na -6 °C.

Vypočtěte ve °C, jaká byla průměrná denní teplota.
Řešení
Průměrná denní teplota byla 3,75 °C.
Matematická úloha – Průměrná denní teplota

90. Číselná osa

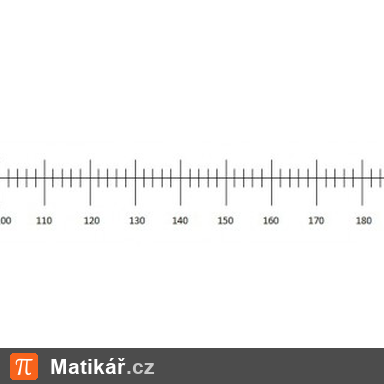
Je dána číselná osa a na ní jsou vyznačena čísla 258 a 326.

Vypočítejte, které číslo leží na číselné ose přesně ve středu mezi těmito čísly.
Řešení
Ve středu mezi zadanými čísly leží číslo 292.
Matematická úloha – Číselná osa

91. Obsah kosočtverce

Obvod kosočtverce, který má délky úhlopříček v poměru 3:4 je 40 cm.

Vypočtěte, kolik cm2 je jeho obsah.
Řešení
Obsah kosočtverce je 96 cm2
Matematická úloha – Obsah kosočtverce

92. Válcová nádrž

Nádrž tvaru válce o průměru 100 cm je naplněná z 50 % a je v ní 78 500 l vody.

Vypočítejte, jaká je výška nádrže. (Zaokrouhlete na celé metry.)
Řešení
Výška nádrže je 50 m.
Matematická úloha – Válcová nádrž

93. Vypočítejte zlomky

Vypočítejte:
a)    z 8
b)    ze 39
c)    z 56
d)    z 45
e)    z 42
f)    z 21
Řešení
a)   2
b)   13
c)   8
d)   18
e)   35
f)   9
Matematická úloha – Vypočítejte zlomky

94. Objem krabice

Krabice má výšku 55 cm a šířku 40 cm. Objem krabice je 180 litrů.

Vypočtěte
a)   a na dvě desetinná místa zapište, kolik cm měří délka krabice,
b)   kapacitu krabice v cm3.
Řešení
a)   Délka krabice je 81,82 cm.
b)   Objem krabice je 180 000 cm3
Matematická úloha – Objem krabice

95. Náhodné autobusy

Ve městě Náhoda zrušily jízdní řády a autobusy MHD jezdí zcela náhodně. Představte si, že stojíte na zastávce, na které zastavuje 5 autobusů s čísly 12, 14, 15, 21 a 27 a vy se dvěma z nich můžete dostat domů.

Vypočtěte v procentech:
a)   jaká je pravděpodobnost, že se můžete dostat domů hned prvním autobusem, který přijede,
b)   jaká je pravděpodobnost, že se nemůžete dostat domů hned prvním autobusem, který přijede,
c)   jaká je pravděpodobnost, že jako první přijede autobus, jehož číslo je dělitelné třemi.
Řešení
a)   Pravděpodobnost je 40 %.
b)   Pravděpodobnost je 60 %.
c)   Pravděpodobnost je 80 %.
Matematická úloha – Náhodné autobusy

96. Zvětšení kruhu

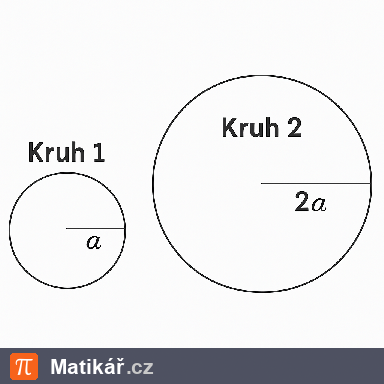
Kruh 1 má poloměr a. Kruh 2 má poloměr dvakrát větší.

Vypočtěte, kolikrát větší má kruh 2 větší než kruh 1:
a)   průměr.
b)   obvod,
c)   obsah.
Řešení
a)   Kruh 2 má 2krát větší průměr než kruh 1.
b)   Kruh 2 má 2krát větší obvod než kruh 1.
c)   Kruh 2 má 4krát větší obsah než kruh 1.
Matematická úloha – Zvětšení kruhu

97. Hromy, blesky

Zvuk se šíří rychlostí 1 km za 3 sekundy. Hrom bylo slyšet 12 sekund po blesku.

Vypočtěte v kilometrech, v jaké vzdálenosti je bouře.
Řešení
Bouře je ve vzdálenosti 4 km.
Matematická úloha – Hromy, blesky

98. Účet v bance

Na účtu v bance bylo 6 600 Kč, za což byl na konci roku připsán úrok 330

Vypočtěte, kolik procent byla úroková míra.
Řešení
Úroková míra byla 5 %.
Matematická úloha – Účet v bance

99. Procenta části celku

Vypočtěte, kolik procent je čtvrtina dvou pětin celku.
Řešení
Čtvrtina dvou pětin celku je 10 %.
Matematická úloha – Procenta části celku

100. Výlet na kole

Olga jela na projížďku na kole. Za hodinu se za ní po stejné trase vypravil bratr na motorce stálou rychlostí 60 km/h a dojel ji za hodiny.

Určete:
a)   v km délku trasy, kterou Olga ujela, než ji bratr dojel,
b)   v kilometrech za hodinu, jakou průměrnou rychlostí Olga jela.
Řešení
a)   Olga ujela 30 km.
b)   Olga jela rychlostí 20 km/h.
Matematická úloha – Výlet na kole
 
34567