Úlohy: 61–80 / 140

23456
Přehled ročníků

61. Sčítání a odčítání zlomků 3

Sečtěte a odečtěte zlomky:
a)   
b)   
c)   
d)   
e)   
f)   
g)   
h)   
i)   
j)   
k)   
l)   
Řešení
a)   
b)   
c)   
d)   
e)   
f)   
g)   
h)   
i)   
j)   
k)   
l)   

62. Sčítání a odčítání zlomků 2

Sečtěte a odečtěte zlomky:
a)   
b)   
c)   
d)   
e)   
f)   
g)   
h)   
i)   
j)   
k)   
l)   
Řešení
a)   
b)   
c)   
d)   
e)   
f)   
g)   
h)   
i)   
j)   
k)   
l)   

63. Neznámý zlomek

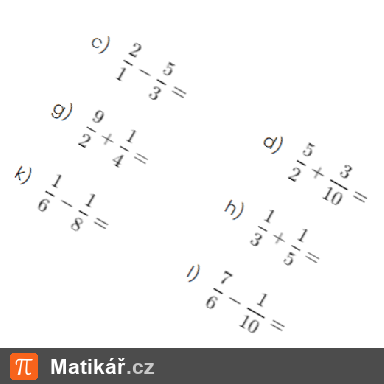
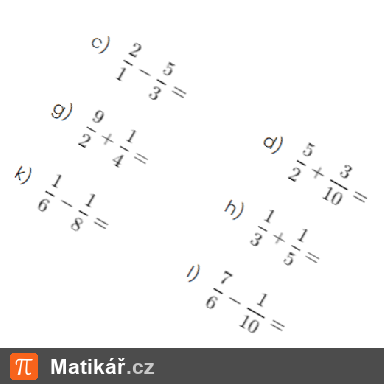
Je dán zlomek, jehož jmenovatel je o 2 větší než jeho čitatel. Když čitatele i jmenovatele tohoto zlomku zvětšíme o 7, obdržíme zlomek .

Určete základní tvar hledaného zlomku.
Řešení
Čitatel hledaného zlomku je 3 a jmenovatel hledaného zlomku je 5.

64. Hod kostkou a mincí

Hodíme kostkou a pak hodíme tolikrát mincí, jaké číslo padlo na kostce.

Vypočítejte v procentech, jaká je pravděpodobnost, že padne na minci alespoň jednou hlava.
Řešení
Pravděpodobnost je 83,59 procent.

65. Kapacita hotelu

V hotelu bydlí polovina lidí v prvním patře, třetina ve druhém patře a zbylých 40 hostů v podkroví. Hotel je obsazen ze 75 %.

Vypočítejte kapacitu hotelu.
Řešení
Kapacita hotelu je 320 hostů.

66. Výroba másla

Průměrně se ze 100 litrů mléka vyrobí 16 litrů smetany a ze 100 litrů smetany se vyrobí 20 litrů másla.

Vypočítejte, kolik litrů mléka je potřeba na výrobu 100 litrů másla.
Řešení
Na výrobu 100 litrů másla je potřeba 3 125 litrů mléka.

67. Jízda automobilu po okruhu

Automobil projel jeden okruh neznámou stálou rychlostí, další dva stejné okruhy stálou rychlostí 72 km/hod. Celková průměrná rychlost byla 36 km/hod.

Určete rychlost, kterou automobil projel poprvé okruh.
Řešení
Automobil projel poprvé okruh rychlostí 18 km/hod.

68. Učení Petra a Simony

Petr se učil o čtvrtinu času více než Simona. Dohromady se učili 2 hodiny a 51 minut.

Vypočítejte, kolik minut se učil Petr a kolik Simona.
Řešení
Petr se učil 95 minut a Simona 76 minut.

69. Hmotnost boxera

Boxer normálně zápasí s váhou 80 kilogramů. Chce přidat dostatečnou váhu, aby se posunul do kategorie pro 84 kilogramů.

Určete, kolik procent své aktuální tělesné hmotnosti musí přibrat.
Řešení
Boxer musí přibrat 5 procent své aktuální hmotnosti.

70. Krejčí šije roušky

Krejčí potřebuje na obšití roušky metru nitě. Má k dispozici 24 metrů nitě.

Vypočítejte, kolik roušek může krejčí obšít.
Řešení
Krejčí může obšít 40 roušek.

71. Velikost procent

Určete, jestli může být 1 % větší než 2 %.
Řešení
Ano může, platí pro záporná čísla.

72. Cyklistický závod

Cyklisté při závodě ujeli z celkové délky a do cíle jim zbývá 72 km.

Určete:
a)   jak dlouhý byl závod,
b)   kolik procent závodu budou mít cyklisté za sebou po ujetí 94,50 kilometrů.
Řešení
a)   Závod byl dlouhý 126 kilometrů.
b)   Cyklisté budou mít za sebou 75 procent závodu.
c)   

73. Lektvar věčného mládí

Čarodějnice připravuje lektvar věčného mládí. V receptu se dočetla, že objem lektvaru je tvořen ze dvou devítin z tekutého jedu ropuchy, z šesti patnáctin z nektaru mandragory a zbytek tvoří 34 mililitrů vody.

Vypočtěte, kolik mililitrů lektvaru čarodějnice podle tohoto receptu vyrobí.
Řešení
Čarodějnice připraví 90 ml lektvaru věčného mládí.

74. Cyklistický výlet

Emil chce jet na 4 dny na cyklistický výlet. Celkem má v plánu ujet 120 km. První den plánuje ujet čtvrtinu celé trasy. Druhý den , třetí den chce ujet celé trasy výletu.

Vypočítejte:
a)   kolik kilometrů Emil ujede za první 3 dny,
b)   kolik kilometrů Emilovi zbyde na poslední den.
Řešení
a)   Za první tři dny Emil ujede 88 km.
b)   Na poslední den Emilovi zbyde 32 km.

75. Jardova oslava

Na oslavu Jardových narozenin se sešlo 24 hostů. Polovina z nich byli bývalí spolužáci, čtvrtina byli spoluhráči z fotbalu a třetina byli sousedi.

Vypočtěte:
a)   kolik hostů byli bývalí spolužáci,
b)   kolik hostů byli spoluhráči z fotbalu,
c)   kolik hostů byli sousedi.
Řešení
a)   12 hostů byli bývalí spolužáci.
b)   6 hostů byli spoluhráči z fotbalu.
c)   8 hostů byli sousedi.

76. Aritmetická posloupnost

V aritmetické posloupnosti je dáno a1=4, Sn=589, d=3.

Vypočtěte, kolik členů má aritmetická posloupnost.
Řešení
Aritmetická posloupnost má 19 členů.

77. Sčítání a odčítání zlomků 1

Sečtěte a odečtěte zlomky:
a)   
b)   
c)   
d)   
e)   
f)   
g)   
h)   
i)   
j)   
k)   
l)   
Řešení
a)   
b)   
c)   
d)   
e)   
f)   
g)   
h)   
i)   
j)   
k)   
l)   

78. Maso během diety

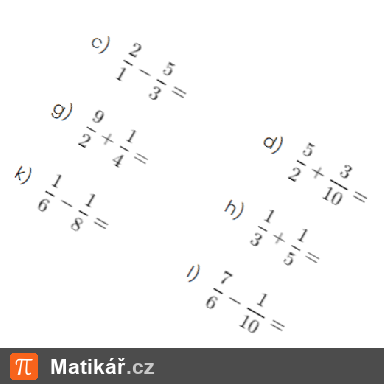
Paní Tučná chce zhubnout v lednici má maso o hmotnosti kilogramu. Paní Tučná má však povoleno sníst v rámci diety pouze kilogramu masa.

Vypočítejte, jakou část masa může paní Tučná sníst, aby dodržela svoji dietu.
Řešení
Paní Tučná může sníst 3/4 masa.

79. Červené a bílé kuličky

Máme 15 červených a 5 bílých kuliček.

Vypočítejte v procentech, jaká je pravděpodobnost, že první vytažená kulička bude bílá.
Řešení
Pravděpodobnost, že první vytažená kulička bude bílá, je 25 %.

80. Obvod trojúhelníku ABC

Je dán trojúhelník ABC. Délka strany a je rovna dvou třetinám strany c. Délka strany c je rovna třem pětinám délky strany b. Délka strany b je 15 cm.

Vypočítejte obvod trojúhelníku ABC.
Řešení
Obvod trojúhelníku ABC je 50 cm.
 
23456