Matikář - Úlohy na procvičení

Úlohy: 141–160 / 190

Určete nejmenší přirozené číslo $ x $ takové, že $ 2x $ je druhá mocnina přirozeného čísla a $ 3x $ je třetí mocnina přirozeného čísla.

Řešení

x = 72

Matematická úloha – Myšlené přirozené číslo

142. Obsah trojúhelníku

Je dán trojúhelník ABC. Jeho obvod je 30 cm, přičemž strana a je o 2 cm delší než strana b a o 5 cm kratší než strana c.

Určete obsah trojúhelníku v cm² a zaokrouhlete na dvě desetinná místa.

Řešení

Obsah trojúhelníku 26,83 cm²

143. Seskok na Zemi a na Měsíci

Za bezpečný seskok je považován takový, při kterém člověk dopadne na zem maximální rychlostí 8 m/s. Zrychlení na Zemi je g = 10 ms^-2 a zrychlení na Měsíci je 6krát menší než na Zemi.

Určete v metrech (na jedno desetinné místo) maximální výšku, ze které lze bezpečně skočit na Zemi a na Měsíci.

Řešení

a) Na Zemi lze bezpečně skočit z výšky 3,20 m,

b) na Měsíci z výšky 19,20 m.

Matematická úloha – Seskok na Zemi a na Měsíci

144. Vnitřní úhly trojúhelníku

Na hodinovém ciferníku navzájem spojíme body u čísel 3, 10 a 12, čímž vznikne trojúhelník.

Vypočítejte velikosti vnitřních úhlů tohoto trojúhelníku

a) u čísla 3,

b) u čísla 10,

c) u čísla 12.

Řešení

a) Velikost úhlu u čísla 3 je 30 °.

b) Velikost úhlu u čísla 10 je 45 °.

c) Velikost úhlu u čísla 12 je 105 °.

Matematická úloha – Vnitřní úhly trojúhelníku

145. Úhly v lichoběžníku

O úhlech v lichoběžníku ABCD je známo: velikost úhlu $ \gamma $ je 121 °, velikost úhlu $ \alpha $ je 2/3 úhlu $ \delta $.

Vypočítejte rozdíl úhlů $ \alpha $ a $ \beta $.

Řešení

Rozdíl úhlů $ \alpha $ a $ \beta $ je 13 °.

146. Pochodující hlídka

Hlídka měla určený pochodový úhel 13 °. Po ujetí 9 km se úhel změnil na 62 °. Tímto směrem šla hlídka 10 km.

Vypočítejte v km, jaká je vzdušnou čarou vzdálenost startu a cíle pochodu hlídky. (Zapište na dvě desetinná čísla.)

Řešení

Vzdálenost startu a cíle pochodu byla 17,29 km.

147. Házení kostkou

Karel hodil dvakrát hrací kostkou.

Vypočtěte v procentech, jaká je pravděpodobnost, že součet obou hodů je 11. (Výsledek zapište na dvě desetinná místa.)

Řešení

Pravděpodobnost je 5,56 %.

148. Dvě hrací kostky

Pavel hodil najednou dvěma hracími kostkami.

Vypočtěte v procentech, jaká je pravděpodobnost, že součet na kostkách bude 12. (Výsledek zapište na dvě desetinná místa.)

Řešení

Pravděpodobnost je 2,78 %.

149. Ochlazení vody

Vypočítejte hmotnost vody v kilogramech, která při ochlazení ze 69 °C na 27 °C odevzdala 520,50 kJ tepla. (Zapište na dvě desetinná místa.)

Řešení

Hmotnost vody je 2,96 kg.

150. Černý pasažér

V autobuse cestuje 32 cestujících, z toho tři pasažéři bez platné jízdenky. Do autobusu nastoupil revizor a začal cestující kontrolovat.

Vypočtěte v procentech, jaká je pravděpodobnost, že až druhý cestující, kterého revizor zkontroluje, bude bez platné jízdenky.

Řešení

Pravděpodobnost je 8,77 %.

151. Bonbony v sáčku

V neprůhledném balíčku je 5 citronových, 6 jablečných a 3 jahodové bonbóny.

Vypočtěte, kolik nejméně bonbonů musíme vybrat, aby byl mezi nimi určitě alespoň jeden jahodový.

Řešení

Musíme vytáhnout 12 bonbonů.

152. Řeka viditelná z rozhledny

Z rozhledny, která je 15 m vysoká a od řeky vzdálená 30 m, vidíme řeku pod výškovým úhlem 15 °.

Vypočtěte šířku řeky v metrech a zapište na jedno desetinné místo.

Řešení

Řeka je široká 43,30 metrů.

Matematická úloha – Řeka viditelná z rozhledny

153. Oprava střechy věže

Střecha věže má tvar pravidelného čtyřbokého jehlanu a výškou 4 m a hranou podstavy 6 m. Zjistilo se, že je poškozeno 25 % krytiny na střeše.

Vypočtěte, kolik metrů čtverečních krytiny je potřeba k opravě střechy.

Řešení

K opravě je třeba 15 m² krytiny.

154. Řazení vagónů

Vypočítejte, kolika způsoby můžeme seřadit 5 vagonů, když ve třech vagonech je písek a ve dvou je cement.

Řešení

Vagóny můžeme seřadit 10 způsoby.

155. Zvětšení kruhu

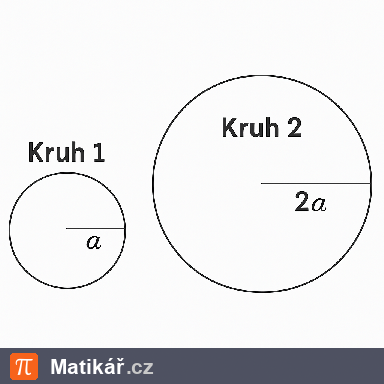
Kruh 1 má poloměr a. Kruh 2 má poloměr dvakrát větší.

Vypočtěte, kolikrát větší má kruh 2 větší než kruh 1:

a) průměr.

b) obvod,

c) obsah.

Řešení

a) Kruh 2 má 2krát větší průměr než kruh 1.

b) Kruh 2 má 2krát větší obvod než kruh 1.

c) Kruh 2 má 4krát větší obsah než kruh 1.

156. Student u zkoušky

Při zkoušce si student náhodně vylosuje tři otázky ze 30 možných. K úspěšnému složení zkoušky musí všechny tři otázky správně zodpovědět. Student umí 70 % otázek.

Vypočtěte, jaká je pravděpodobnost, že student u zkoušky uspěje.

Řešení

Pravděpodobnost je 32,78 %.

157. První stupeň školy

Ve škole je na prvním stupni p prvňáků. Druháků je o 18 % méně než prvňáků. Třeťáků je o 7 více než druháků a čtvrťáků je dvakrát více než prvňáků a druháků dohromady.

Vyjádřete výrazem počet žáků na prvním stupni a výraz zjednodušte.

Řešení

Na prvním stupni je 6.28p+7 žáků.

158. Objem jehlanu

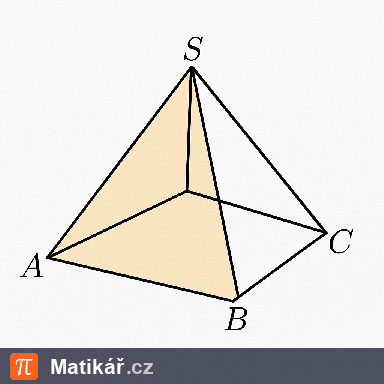
Je dán pravidelný čtyřbokého jehlanu. Výška jehlanu je 30 cm a stěnová výška je 50 cm.

Vypočtěte v dm³ objem jehlanu.

Řešení

Objem jehlanu je 64 dm³.

159. Výrobní linky

V továrně se vyrábí 35 % výrobků na výrobní lince A, která vyrábí zmetky s pravděpodobností $\frac{2}{100}$ a 65 % výrobků na výrobní lince B, kde je pravděpodobnost zmetků $\frac{3}{100}$ .