Máslo a čokoláda stála dohromady 36 Kč. Máslo bylo o 6 Kč dražší než čokoláda.
Kamila cestovala na své první cestě hodiny a na druhé
hodiny.
Obdélník má obsah 145 cm2 a šířku 5 cm.
3 vejce se uvaří za 15 minut.
Čokoláda má na šířku 6 čtverečků, na délku má o polovinu čtverečků více.
Pavlínka s Klárkou mají dohromady 34 bonbonů. Když dá Klárka Pavlínce 2 bonbony, budou mít stejně.
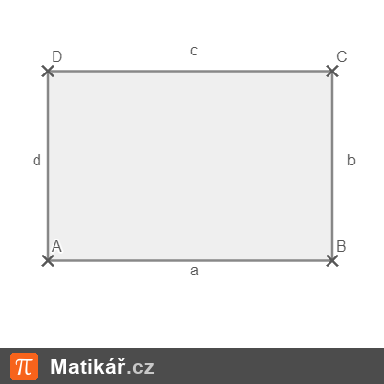
Je dán obdélník ABCD: |AB| = 8 cm a délka úhlopříčky |AC| = 13 cm.
Vytvoření 4 výrobků trvá celkem 80 hodin. Každý výrobek vyrábějí stejně dlouho.
Prodavač prodal 27 kg hladké mouky a třikrát méně hrubé mouky.
Jedna strana obdélníku má délku 18 cm. Obvod obdélníku je 48 cm.
Děti na škole v přírodě byly ubytovány v hotelu 17 dvoulůžkových a 25 třílůžkových pokojích. Další děti byly ubytovány v 8 chatkách. V každé chatce byl 1 čtyřlůžkový a 1 třílůžkový pokoj. Všechny pokoje a postele byly obsazeny.
Martina a Alena mají dohromady 114 bonbónů. Martina má 5krát více než Alena.
Na záchranu 160 stromů je třeba nasbírat 25 tun tříděného papíru.
Je dáno číslo 123 456 789
Na oslavu Jardových narozenin se sešlo 24 hostů. Polovina z nich byli bývalí spolužáci, čtvrtina byli spoluhráči z fotbalu a třetina byli sousedi.
Zahradník zasadil do řady 5 stromečků pravidelně 4 metry od sebe.
Na stole jsou dvě krabice pizzy stejné velikosti. V jedné krabici je pizzy a ve druhé
pizzy. Potom kuchař rozdělí obě pizzy na dílky tak, že jeden dílek je
pizzy.
Kamila má v pokladničce 90 Kč. Její kamarádka Eva má 5krát více.
Po 30 km je cyklista v jedné pětině závodu.
