Úlohy: 1–20 / 143

12345
Přehled ročníků

1. Dělení se zbytkem 1

Vypočítejte následující úlohy:
a)   \( 1234 : 45 = \)
b)   \( 2468 : 78 = \)
c)   \( 3571 : 56 = \)
d)   \( 4825 : 34 = \)
e)   \( 5921 : 67 = \)
f)   \( 8143 : 89 = \)
g)   
Řešení
a)   27 zbytek 19
b)   31 zbytek 50
c)   63 zbytek 43
d)   141 zbytek 1
e)   88 zbytek 25
f)   91 zbytek 52

2. Součin dvouciferných čísel 2

Vypočítejte následující úlohy:
a)   \( 34 \cdot 42 = \)
b)   \( 46 \cdot 35 = \)
c)   \( 58 \cdot 47 = \)
d)   \( 63 \cdot 39 = \)
e)   \( 72 \cdot 48 = \)
f)   \( 81 \cdot 53 = \)
Řešení
a)   1428
b)   1610
c)   2726
d)   2457
e)   3456
f)   4293

3. Součin dvouciferných čísel 1

Vypočítejte následující úlohy:
a)   \( 12 \cdot 15 = \)
b)   \( 23 \cdot 11 = \)
c)   \( 34 \cdot 21 = \)
d)   \( 45 \cdot 12 = \)
e)   \( 56 \cdot 14 = \)
f)   \( 67 \cdot 13 = \)
Řešení
a)   180
b)   253
c)   714
d)   540
e)   784
f)   871

4. Dělení do sta 2

Vypočítej následující úlohy:
a)   \( 54 : 6 = \)
b)   \( 63 : 7 = \)
c)   \( 72 : 9 = \)
d)   \( 81 : 9 = \)
e)   \( 56 : 8 = \)
f)   \( 64 : 8 = \)
Řešení
a)   9
b)   9
c)   8
d)   9
e)   7
f)   8

5. Dělení do sta 1

Vypočítej následující úlohy:
a)   \( 18 : 3 \) =
b)   \( 21 : 7 \) =
c)   \( 16 : 2 \) =
d)   \( 27 : 9 \) =
e)   \( 14 : 7 \) =
f)   \( 36 : 6 \) =
Řešení
a)   6
b)   3
c)   8
d)   3
e)   2
f)   6

6. Sčítání dvouciferných čísel 3

Vypočítejte úlohy:
a)   65 + 27 =
b)   48 + 39 =
c)   53 + 18 =
d)   76 + 24 =
e)   82 + 17 =
f)   69 + 31 =
Řešení
a)   92
b)   87
c)   71
d)   100
e)   99
f)   100

7. Sčítání dvouciferných čísel 2

Vypočítejte úlohy:
a)   62 + 47 =
b)   85 + 39 =
c)   73 + 18 =
d)   49 + 56 =
e)   77 + 44 =
f)   68 + 25 =
Řešení
a)   109
b)   124
c)   91
d)   105
e)   121
f)   93

8. Sčítání dvouciferných čísel 1

Vypočítejte úlohy:
a)   47 + 36 =
b)   58 + 29 =
c)   62 + 18 =
d)   73 + 47 =
e)   84 + 56 =
f)   91 + 32 =
Řešení
a)   83
b)   87
c)   80
d)   120
e)   140
f)   123

9. Po sobě jdoucí čísla

Součet pěti po sobě jdoucích sudých čísel je -10 .

Určete nejvyšší z čísel.
Řešení
Nejvyšší z těchto čísel je 2.

10. Hodnota výrazu

Vypočítej hodnotu výrazu y = 3x2 – 2x + 3 pro:
a)   x = -2,
b)   x = 1,
c)   x = 0,
d)   x = 0,50.
Řešení
a)   19
b)   -2
c)   3
d)   2,75

11. Oslava narozenin tety a srýce

Strýc Anety má narozeniny ve stejný den v roce jako Anetčina teta. Strýc je starší než teta, ne však o víc než o 10 let, a oba jsou plnoletí (starší než 18 let). Na poslední oslavě jejich narozenin si Aneta uvědomila, že když vynásobí jejich oslavované věky a výsledný součin ještě vynásobí počtem psů, kteří se na oslavě sešli, dostane číslo 2 024.

Určete. kolik psů mohlo být na této oslavě. (Uveďte všechny možnosti.)
Řešení
Na oslavě může být 1 pes nebo 4 psi.

12. Trika a sukně

Karolína si koupila 5 trik a 2 mikiny. Jedno triko stálo 250 Kč. Karolína celkem zaplatila 2 210 Kč.

Vypočítejte, kolik Kč stála jedna mikina.
Řešení
Jedna mikina stála 480 Kč.

13. Jízdní kola a tříkolky

V prodejně mají 6 jízdních kol a 5 tříkolek.

Vypočítejte, kolik mají jízdní kola a tříkolky v prodejně dohromady kol.
Řešení
Jízdní kola a tříkolky v prodejně mají dohromady 27 kol.

14. Absolutní hodnota

Vypočítejte
a)   
b)   
c)   
d)   
e)   
f)   
Řešení
a)   16
b)   8
c)   19
d)   28
e)   7
f)   19

15. Absolutní hodnota

Vypočítejte
a)   
b)   
c)   
d)   
e)   
f)   
Řešení
a)   14
b)   9
c)   5
d)   32
e)   32
f)   11

16. Aritmetický průměr šesti čísel

Aritmetický průměr šesti čísel je 80. Prvních pět čísel je 55, 74, 11, 87 a 69.

Určete šesté číslo.
Řešení
Šesté číslo je 184.

17. Zkrácení prkna

Prkno dlouhé m bylo zkráceno o m.

Vypočítejte, jak dlouhé bylo prkno po odříznutí.
Řešení
Prkno bylo dlouhé m.

18. Vlastnosti rovnoramenného trojúhelníku

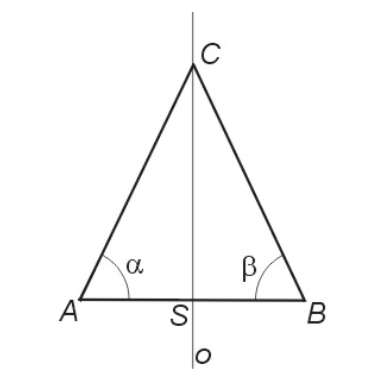
V rovnoramenném trojúhelníku je délka ramene 25 cm, výška trojúhelníku je 24 cm.

Vypočítejte:
a)   délku základny v centimetrech,
b)   obvod trojúhelníku v centimetrech,
c)   obsah trojúhelníku v centimetrech čtverečných.
Řešení
a)   Délka základny je 14 cm.
b)   Obvod trojúhelníku je 64 cm.
c)   Obsah trojúhelníku je 168 cm².

19. Petr zaplatil

Tomáš zaplatil za 12 koláčů 288 Kč.

Vypočítejte, kolik by zaplatil za 15 stejných koláčů.
Řešení
Tomáš by zaplatil 360 Kč.

20. Pět hodů mincí

Vypočítejte, jaká je pravděpodobnost, že při hodu mincí 5× po sobě padne hlava. (Výsledek zapište ve tvaru zlomku.)
Řešení
Pravděpodobnost je .
 
12345