Matikář - Úlohy na procvičení

Úlohy: 241–260 / 366

V okně jsou dvě skleněné tabule, každá o rozměrech 75 cm × 120 cm a tloušťce 2 mm. Jeden metr krychlový skla má hmotnost 2 500 kilogramů.

Vypočtěte v kilogramech hmotnost skleněných tabulí v okně.

Řešení

Skleněné tabule mají hmotnost 9 kilogramů.

242. Dělitelnost

Je dáno číslo 123 456 789

a) Určete jednu číslici, kterou je třeba vynechat, aby vzniklo co největší číslo dělitelné třemi.

b) Určete jednu číslici, kterou je třeba vynechat, aby vzniklo co největší číslo dělitelné devíti.

Řešení

a) Je třeba vynechat číslici 3.

b) Je třeba vynechat číslici 9.

243. Čtyřciferná čísla

Najděte:

a) nejmenší čtyřciferné číslo dělitelné šesti,

b) největší čtyřciferné číslo dělitelné šesti.

Řešení

a) Nejmenší čtyřciferné číslo dělitelné šesti je 1 002.

b) Největší čtyřciferné číslo dělitelné šesti 9 996.

244. Dělení peněz

Tři chlapci si měli rozdělit 1 813 Kč. Rozdělili si je v poměru Honza : Matěj 6:5. Matěj : Pavel 2:3.

Vypočtěte, kolik korun dostal každý z chlapců.

Řešení

Honza dostal 588 Kč, Matěj dostal 490 Kč a Pavel dostal 735 Kč.

Emil chce jet na 4 dny na cyklistický výlet. Celkem má v plánu ujet 120 km. První den plánuje ujet čtvrtinu celé trasy. Druhý den $\frac{2}{15}$ , třetí den chce ujet $\frac{7}{20}$ celé trasy výletu.

Vypočítejte:

a) kolik kilometrů Emil ujede za první 3 dny,

b) kolik kilometrů Emilovi zbyde na poslední den.

Řešení

a) Za první tři dny Emil ujede 88 km.

b) Na poslední den Emilovi zbyde 32 km.

246. Strany pravoúhlého trojúhelníku

Poměry stran pravoúhlého trojúhelníku jsou 3:4:5. Obvod trojúhelníka je 48 cm.

Vypočítejte, jak dlouhá je přepona.

Řešení

Přepona je dlouhá 20 cm.

Matematická úloha – Strany pravoúhlého trojúhelníku

247. Tři strážní

Tři strážní mají společnou ostrahu podniku. První vykoná svoji pochůzku za 15 minut, druhý ujde svůj okruh za 10 minut a třetí strážný za 12 minut.

Vypočítejte, za jak dlouho se opět všichni tři potkají, když na začátku vyjdou ze stejného místa.

Řešení

Všichni tři strážní se opět potkají za 60 minut.

248. Mandle

Denní potřeba tuku pro člověka činí v průměru 80 g. Mandle obsahují 45 % tuku.

Vypočtěte, kolik gramů mandlí by musel člověk sníst, aby svou denní potřebu tuků pokryl pouze pojídáním mandlí.

Řešení

Člověk by musel sníst 178 g mandlí.

249. Obsah čtverce

Vypočtěte, o kolik procent se zvětší obsah čtverce, pokud se jeho obvod zvětší o pětinu.

Řešení

Obsah čtverce se zvětší o 44 %.

250. Zmenšení pozemku

Delší rozměr obdélníkového pozemku byl zmenšen o jednu pětinu, kratší o jednu čtvrtinu.

Vypočítejte, o kolik procent se zmenšila plocha pozemku.

Řešení

Plocha pozemku se zmenšila o 40 procent.

251. Dopravní značka hlavní silnice

Dopravní značka hlavní silnice má tvar čtverce s bílým okrajem a žlutým čtvercem uprostřed. Tato dopravní značka má obsah 49 dm². Obsah žlutého čtverce je 2 500 cm².

Vypočítejte v centimetrech šířku bílého pruhu.

Řešení

Bílý pruh je široký 10 cm.

Matematická úloha – Dopravní značka hlavní silnice

252. Dělení platby za zakázku

Tři společníci dostali za provedenou zakázku zaplaceno 90000 Kč. 40 % z této částky stal materiál, 23 % že zbylé částky odvedli za pojištění a daně. Zbytek peněz si rozdělili v poměru 2:3:5.

Vypočítejte, jakou částku dostal každý ze společníků.

Řešení

První společník dostal 8 316 Kč, druhý společník dostal 12 474 Kč a třetí společník dostal 20 790 Kč.

253. Sčítání a odčítání zlomků 1

Sečtěte a odečtěte zlomky:

a) $\frac{3}{2}-\frac{3}{10}=$

b) $\frac{2}{3}+\frac{1}{2}=$

c) $\frac{9}{8}-\frac{1}{2}=$

d) $\frac{6}{5}-\frac{1}{4}=$

e) $\frac{3}{2}-\frac{9}{8}=$

f) $\frac{7}{4}+\frac{9}{8}=$

g) $\frac{9}{2}-\frac{3}{1}=$

h) $\frac{5}{4}-\frac{1}{2}=$

i) $\frac{6}{5}-\frac{1}{6}=$

j) $\frac{1}{1}-\frac{4}{5}=$

k) $\frac{5}{4}+\frac{3}{1}=$

l) $\frac{2}{3}+\frac{3}{10}=$

Řešení

a) $\frac{6}{5}$

b) $\frac{7}{6}$

c) $\frac{5}{8}$

d) $\frac{19}{20}$

e) $\frac{3}{8}$

f) $\frac{23}{8}$

g) $\frac{3}{2}$

h) $\frac{3}{4}$

i) $\frac{31}{30}$

j) $\frac{1}{5}$

k) $\frac{17}{4}$

l) $\frac{29}{30}$

Matematická úloha – Sčítání a odčítání zlomků 1

254. Maso během diety

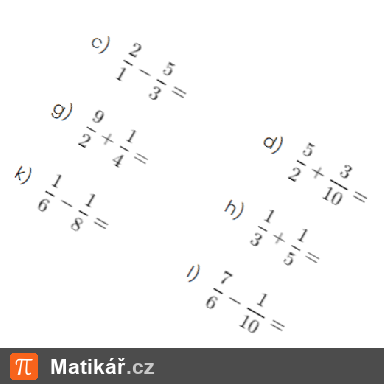
Paní Tučná chce zhubnout v lednici má maso o hmotnosti $\frac{1}{3}$ kilogramu. Paní Tučná má však povoleno sníst v rámci diety pouze $\frac{1}{4}$ kilogramu masa.