Těleso vzniklo tak, že byl do válce o průměru 12 cm a výšce 20 cm vyříznut kužel o stejném průměru a stejné výšce.

Lukáš je o 4 roky starší než jeho sestra Aneta. Před třemi lety byl Lukášův věk dvojnásobkem věku Anety v té době.

V obchodě byly na skladě nové telefony. První den se prodalo 25 % z celkového počtu. Druhý den se prodalo o 40 % více než první den, ale stále zůstalo na skladě ještě 72 kusů telefonů.

Je dán válec s poloměrem základny 6 cm a výškou 10 cm. Na vrcholu tohoto válce je umístěn kužel se stejným poloměrem základny a polovinou výšky válce.

V přístavu jsou kotveny tři lodě: Loď A, loď B a loď C. Loď A veze 2krát více nákladu než loď B a loď C veze o 100 tun méně nákladu než loď A. Celková hmotnost nákladu všech tří lodí je 1 600 tun.

Jsou dány dva trojúhelníky ΔABC a ΔDEF. Je dáno: a = 24 cm, b = 18 cm, c = 36 cm, d = 12 cm, e = 24 cm, f = 16 cm.
Tomáš zapomněl čtyřmístný PIN, pamatuje si první tři čísla. Ví, že čtvrté číslo je liché.

Otec je 3krát starší než syn. Před 6 lety byl otec o 32 let starší než syn.

Obsah obdélníku je 81,25 cm2. Zvětšíme-li jeho délku o 5 mm, zvětší se jeho obsah o 4 %.

Na tři stromy přiletělo 36 sýkorek. Když z prvního stromu přeletělo na druhý
strom 6 sýkorek a z druhého stromu na třetí 4 sýkorky, bylo na všech stromech
stejně sýkorek.

Tříciferné číslo má ciferný součet 16. Pokud v tomto čísle zaměníme číslice na místech stovek a desítek, číslo se o 360 zmenší. Pokud v původním čísle zaměníme čísla na místech desítek a jednotek, číslo se o 54 zvětší.

V kontrolním testu z matematiky je 25 otázek, za každou správnou odpověď se přičte 5 bodů, za každou chybějící nebo chybně zodpovězenou otázku se odečtou 3 body. Jakub dosáhl v tomto testu 69 bodů, přičemž na dvě otázky neodpověděl.

Otec je 3× starší než syn. Za 8 let bude otec o 28 let starší než syn.

V roce 2005 byl otec třikrát tak starý než jeho syn. V roce 2020 byl syn o polovinu mladší než otec.

Tři firmy měly na účtech v bance celkem 3 250 000 Kč. První firma měla o 18 % více peněž než druhá a třetí o 47 000 Kč méně než první.

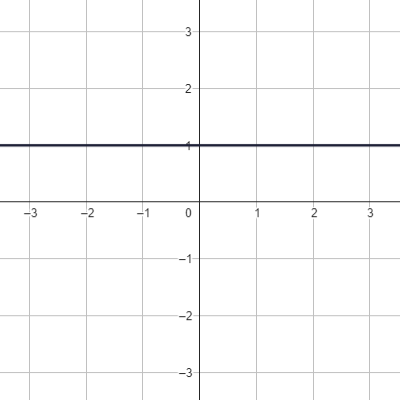
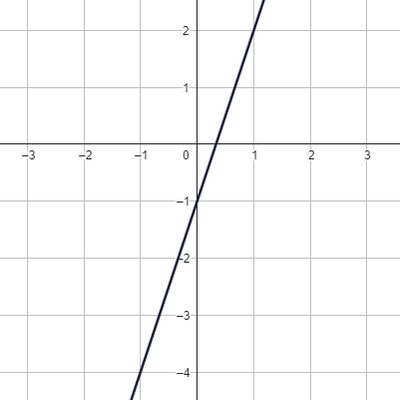
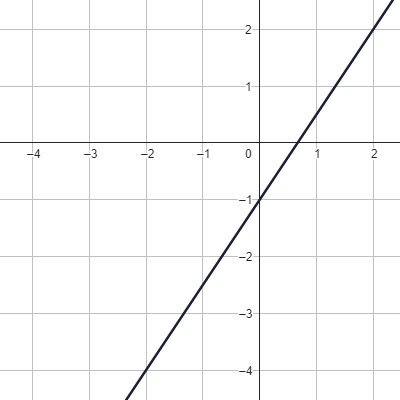
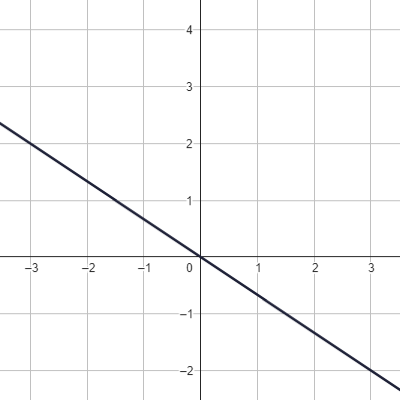
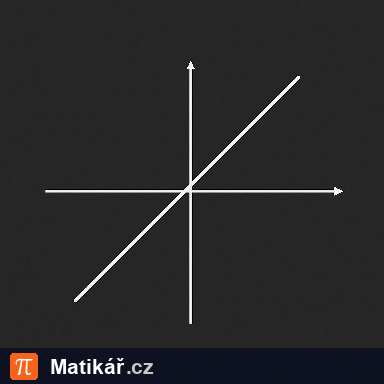
Jsou dány grafy lineárních funkcí.
Bazén ve tvaru kvádru je 50 m dlouhý a 16 m široký. Napustili do něj 12 000 hl vody.

Kamila je 2× starší než Helena. Před 4 roky byla Kamila 6× starší, než tehdy byla Helena.

Ve třídě je 30 žáků. Věk každého počítáme na celé roky. Průměrný věk dívek je 12,25 a chlapců 12,50 a průměrný věk všech je 12,30.

Čelo cyklistického pelotonu jede průměrnou rychlostí 48 km/h. Cyklista se zeleným tričkem ztratil při pádu 5 minut. Chce dosáhnout čelo pelotonu za dvacet minut.
