V hotelu je celkem 50 pokojů, všechny jsou buď 3 lůžkové nebo 5 lůžkové. Kapacita hotelu je 172 hostů.

V hotelu je 200 pokojů, všechny jsou buď 2lůžkové nebo pětilůžkové. Hotel je zcela zaplněn a je v něm 502 hostů.

V malém pytlíku bonbónů jsou 4 bonbóny, ve velkém 7 bonbónů. Na stole leží 12 pytlíků a v nich 63 bonbónů.

Materiál, jehož hmotnost byla 18,20 tun, odvážela tři auta. Druhé vezlo o 20 % více než první a třetí 20 % více než druhé.

Vodní nádrž se vyprázdní samostatně prvním čerpadlem za 12 hodin, druhým za 9 hodin a třetím za 4 hodiny.

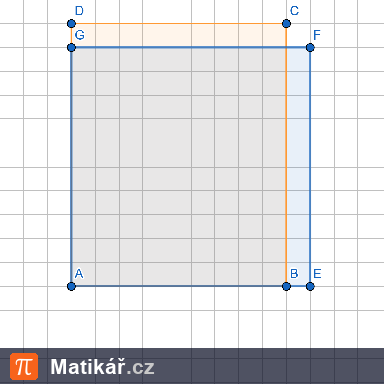
Je dán pravoúhlý trojúhelník ABC s přeponou dlouhou 5 cm a delší odvěsnou dlouhou 4 cm a čtverec KLMN, jehož obvod je stejný velký jako obvod trojúhelníku ABC.

Eva v sobotu ušla za 5 hodin a 30 minut celkem 22 km. Jana během soboty uběhla za 3 hodiny a 40 minut celkem 33 km.

Před rokem byl Honza dvakrát starší než Lenka. Za pět let bude Honza o polovinu starší než Lenka.

Myslím si číslo. Když od něj odečtu jeho jednu třetinu, výsledek vynásobím osmi, získaný součin vydělím třemi a číslo, které mi vyšlo, odečtu od osmi, dostanu číslo čtyři.

Vlak má 4 vagony. Každý vagon kromě prvního veze o 10 % více nákladu než vagon zapojený před ním.

Délka původního obdélníku se zvětšila o 10 % a jeho šířka se o 10 % zmenšila. Tím vznikl nový obdélník.
Odměnu 21 100 korun si 3 pracovníci rozdělili tak, že druhý dostal o 40 % více než první a třetí o 30 % více než druhý.

Prvním postřikovačem se rostliny ošetří za 4 hodiny, druhým za 6 hodin. Postřik probíhal tak, že nejprve první postřikovač pracoval 2 hodiny sám a pak teprve oba současně.

Máme k dispozici 2 litry 20% roztoku.

Do mateřské školky bylo zakoupeno 50 čokolád dvojího druhu – mléčné po 48 Kč za kus, oříškové po 33 Kč za kus. Celkem bylo zaplaceno 2 100 Kč.

Doporučená teplota vody pro koupání nemluvňat je mezi 36 °C. Jana připravila do vaničky 12 litrů vody o teplotě 42 °C. Teplota studené vody z vodovodu je 16 °C.


První slitina je směsí dvou kovů v poměru 1:2, druhá je směsí stejných kovů v poměru 2:3. Chceme získat novou slitinu těchto kovů v poměru 17:27. (Všechny tři poměry odpovídají témuž pořadí obou kovů.)

Petr dokáže udělat celou práci sám za 6 hodin. Martin dokáže udělat stejnou práci sám za 8 hodin. Ve skutečnosti pracoval nejdříve Petr a potom ho vystřídal Martin. Celou práci tak zvládli za 6,50 hodiny. (Žádný z chlapců neměnil své pracovní tempo a střídání chlapců proběhlo bez časové prodlevy.)

První kombajn by úrod z pole sklidil za 7 hodin, druhý za 6 hodin. Kdyby se k nim oběma přidal ještě třetí kombajn, trvala by sklizeň 2 hodiny.
