Bolek a Lolek měli každý svou aritmetickou posloupnost. Jak Lolkova, tak Bolkova posloupnost začínala číslem 2 023 a končila číslem 3 023. Tyto dvě posloupnosti měly 26 společných čísel. Poměr Bolkovy a Lolkovy diference byl 5:2.

Na mapě je skutečná vzdálenost 435 km mezi městy Paříž a Bern vyjádřena úsečkou 15 cm.

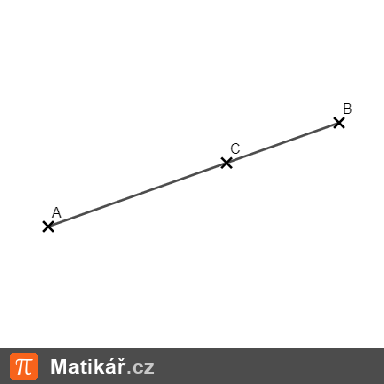
Délka úsečky |AB| = 14 cm. Na úsečce AB je zakreslen bod C tak, že velikosti úseček |AC| a |BC| jsou v poměru 4:3.
Je dáno číslo 123 456 789

Poměry stran pravoúhlého trojúhelníku jsou 3:4:5. Obvod trojúhelníka je 48 cm.


Delší rozměr obdélníkového pozemku byl zmenšen o jednu pětinu, kratší o jednu čtvrtinu.

Tři společníci dostali za provedenou zakázku zaplaceno 90000 Kč. 40 % z této částky stal materiál, 23 % že zbylé částky odvedli za pojištění a daně. Zbytek peněz si rozdělili v poměru 2:3:5.
Je dáno číslo 346



Do taneční přišlo 32 chlapců a 34 dívek.

Z Ananasovic do Banánovic vede 5 cest, z Banánovic do Citrónovic vedou 3 cesty a z Citrónovic do Datlovic vedou 4 cesty.

Učitel napsal na tabuli číslo menší než 50 000.
První žák řekl: "Toto číslo je dělitelné 2."
Druhý žák řekl: "Toto číslo je dělitelné 3."
A tak dále, až po posledního, který tvrdil, že je dělitelné 13. Jeden žák ale lhal.


Učitel vyvolával žáky k tabuli. Ve třídě bylo 25 žáků a pan učitel vyvolal Karla, Sylvu a Josefa.
Petra, Jana a Martin nasbírali maliny v poměru 3:4:2 . Petra nasbírala 4,50 litrů malin.

Obvod kosočtverce, který má délky úhlopříček v poměru 3:4 je 40 cm.
Nádrž tvaru válce o průměru 100 cm je naplněná z 50 % a je v ní 78 500 l vody.

Plat pracovníka byl zvýšen o 8 % nyní je 14 580 Kč.
