Matikář - kategorie úloh

Úlohy: 1–20 / 37

1. Velikost úhlů v trojúhelníku

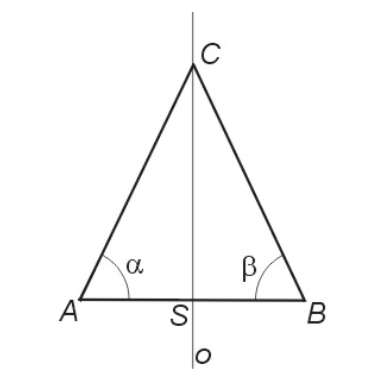
V trojúhelníku je vnitřní úhel \( \beta \) o 20 ° menší než úhel \( \alpha \) a úhel \( \gamma \) je třikrát větší než úhel \( \beta \).

Vypočítejte ve stupních velikost

a) úhlu \( \alpha \),

b) úhlu \( \beta \),

c) úhlu \( \gamma \).

Řešení

a) \( \alpha = 52^\circ \)

b) \( \beta = 32^\circ \)

c) \( \gamma = 96^\circ \)

Matematická úloha – Velikost úhlů v trojúhelníku

2. Trojúhelník a čtverec

Je dán pravoúhlý trojúhelník ABC s přeponou dlouhou 5 cm a delší odvěsnou dlouhou 4 cm a čtverec KLMN, jehož obvod je stejný velký jako obvod trojúhelníku ABC.

Vypočítejte,

o kolik cm² větší či menší je obsah čtverce KLMN oproti trojúhelníku ABC.

Řešení

Obsah čtverce KLMN je o 3 cm² větší než obsah trojúhelníku ABC.

Matematická úloha – Trojúhelník a čtverec

3. Velikosti úhlů v trojúhelníku

V trojúhelníku je vnitřní úhel \(\beta\) o 20° menší než úhel \(\alpha\) a úhel \(\gamma\) je třikrát větší než úhel \(\beta\).

Vypočítejte velikost

a) úhlu \(\alpha\),

b) úhlu \(\beta\),

c) úhlu \(\gamma\).

Řešení

a) \(\alpha = 52^\circ\),

b) \(\beta = 32^\circ\),

c) \(\gamma = 96^\circ\).

Matematická úloha – Velikosti úhlů v trojúhelníku

4. Strany trojúhelníku

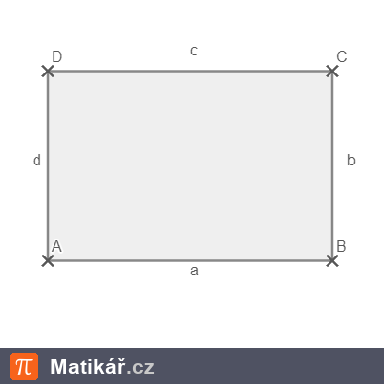
Obvod trojúhelníku je 87 cm. Strana \(a\) je o 15 cm kratší než strana \(b\) a strana \(c\) je o 12 cm delší než strana \(b\).

Vypočítejte v centimetrech délku

a) strany \(a\),

b) strany \(b\),

c) strany \(c\).

Řešení

a) Délka strany \(a\) je 15 cm.

b) Délka strany \(b\) je 30 cm.

c) Délka strany \(c\) je 42 cm.

5. Délky stran trojúhelníku

Obvod trojúhelníku je roven 205 cm. Strana \( b \) je dvakrát delší než strana \( a \), strana \( c \) je o 35 cm kratší než strana \( b \).

Vypočítejte délku

a) strany \( a \),

b) strany \( b \),

c) strany \( c \).

Řešení

a) Strana \( a \) má délku 48 cm,

b) strana \( b \) má délku 96 cm,

c) strana \( c \) má délku 61 cm.

Matematická úloha – Délky stran trojúhelníku

6. Úhly v trojúhelníku

Určete velikosti všech úhlů v trojúhelníku, který je zadán souřadnicemi tří bodů. Výsledky zapište ve stupních na dvě desetinná místa.

a) \( A(1, 2), \quad B(4, 6), \quad C(7, 2). \)

b) \( A(-2, 1), \quad B(3, 4), \quad C(1, -3). \)

c) \( A(2, 3), \quad B(6, 3), \quad C(6, 7). \)

d) \( A(1, 1), \quad B(4, 5), \quad C(7, 2). \)

Řešení

a) \[ \alpha \approx 53.13^\circ, \quad \beta \approx 73.74^\circ, \quad \gamma \approx 53.13^\circ.\]

b) \[ \alpha \approx 79.1^\circ, \quad \beta \approx 50.9^\circ, \quad \gamma \approx 50^\circ. \]

c) \[ \alpha = 45^\circ, \quad \beta = 45^\circ, \quad \gamma = 90^\circ. \]

d) \[ \alpha \approx 48.6^\circ, \quad \beta \approx 60^\circ, \quad \gamma \approx 71.4^\circ. \]

7. Obvod trojúhelníku

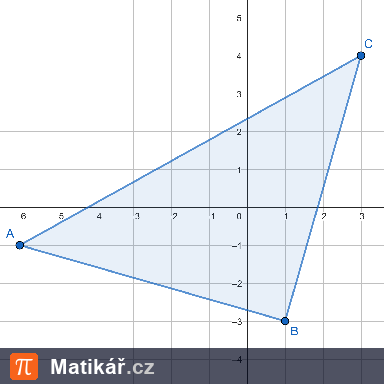
Obvod trojúhelníku ABC je 109 cm. Strana \( b \) je o 10 cm větší než strana \( a \). Strana \( c \) je o 6 cm delší než strana \( a \).

Vypočítejte, kolik cm měří strana \( b \).

Řešení

Strana \( b \) měří 41 cm.

8. Úhlopříčky v rovnoběžníku

Je dán rovnoběžník KLMN, ve kterém známe velikosti stran \( a = |KL| = 84,5 \, \mathrm{cm} \), \( d = |KN| = 47,8 \, \mathrm{cm} \) a velikost úhlu \( \alpha = \angle NKL = 56^\circ 40' \).

Vypočítejte v centimetrech velikost

a) úhlopříčky \( e = |KM| \),

b) úhlopříčky \( f = |LN| \).

Řešení

a) Úhlopříčka e je dlouhá 99,86 cm.

b) Úhlopříčka f je dlouhá 166,52 cm.

Matematická úloha – Úhlopříčky v rovnoběžníku

9. Rozhodni o podobnosti

Jsou dány trojúhelníky:

∆ ABC: a = 9 m, b = 17 m, c = 12 m,

∆ DEF: d = 207 dm, e = 341 dm, f = 394 dm.

Rozhodněte, jestli jsou trojúhelníky podobné.

Řešení

a) 0

b) 1

Matematická úloha – Rozhodni o podobnosti

10. Vystřižené rovnoramenné trojúhelníky

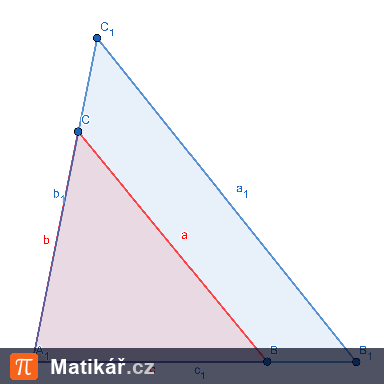
Jsou dány dva shodné rovnoramenné trojúhelníky, z nichž každý má obvod 100 cm. Nejprve z těchto trojúhelníků složíme rovnoběžník tak, že je k sobě přiložíme rameny. Poté z nich složíme kosočtverec tak, že je k sobě přiložíme základnami. Rovnoběžník má o 4 cm kratší obvod než kosočtverec.

Vypočítejte délky stran trojúhelníků.

Řešení

Základna má délku 32 cm, rameno má délku 34 cm.

Matematická úloha – Vystřižené rovnoramenné trojúhelníky

11. Vlastnosti rovnoramenného trojúhelníku

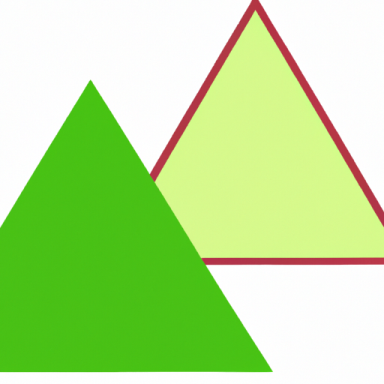
V rovnoramenném trojúhelníku je délka ramene 25 cm, výška trojúhelníku je 24 cm.

Vypočítejte:

a) délku základny v centimetrech,

b) obvod trojúhelníku v centimetrech,

c) obsah trojúhelníku v centimetrech čtverečných.

Řešení

a) Délka základny je 14 cm.

b) Obvod trojúhelníku je 64 cm.

c) Obsah trojúhelníku je 168 cm².

Matematická úloha – Vlastnosti rovnoramenného trojúhelníku

12. Cesty v parku

Cesty v parku tvoří pravoúhlý trojúhelník, jehož odvěsny mají na plánku s měřítkem 1:200 rozměry délek stran 9 cm a 12 cm. Babička chodí každý den po této trase na zdravotní procházku.

Vypočítejte

a) kolik m² zabírá plocha ohraničená těmito cestami,

b) kolikrát musí babička projít všechny tři cesty, aby nachodila alespoň 1,50 km.

Řešení

13. Úhly v rovnoběžníku

Je dán rovnoběžník ABCD, délka jeho jedné úhlopříčky je rovna délce jeho jedné strany.

Vypočítejte, jakou velikost mají vnitřní úhly rovnoběžníku ABCD.

Řešení

Vnitřní úhly rovnoběžníku ABCD mají velikost 60 ° a 120 °.

14. Podobnost trojúhelníků

Trojúhelník ABC a trojúhelník ADE jsou podobné. Délka strany DE je 12 cm, délka strany BC je 16 cm a obsah trojúhelníku ADE je 27 cm².

Vypočítejte v centimetrech čtverečních obsah trojúhelníku ABC.

Řešení

Obsah trojúhelníku ABC je 48 cm².

Matematická úloha – Podobnost trojúhelníků

15. Pozemek tvaru lichoběžníku

Pozemek tvaru pravoúhlého lichoběžníku má základny dlouhé 102 m a 86 m. Kolmé rameno má délku 63 m.

Vypočítejte

a) obsah pozemku,

b) obvod pozemku.

Řešení

a) Obsah pozemku je 5 922 m²m

b) obvod pozemku 316 metrů.

Matematická úloha – Pozemek tvaru lichoběžníku

16. Pravoúhlý trojúhelník

Délky stran pravoúhlého trojúhelníku tvoří první 3 členy aritmetické posloupnosti. Obsah trojúhelníku je 600 cm².

Určete délky stran trojúhelníku.

Řešení

Délky stran trojúhelníku podle velikosti jsou 30 cm, 40 cm a 50 cm.

Matematická úloha – Pravoúhlý trojúhelník

17. Trojboký hranol

Pravidelný trojboký hranol má délku podstavné hrany a = 6 cm a jeho výška je rovna délce podstavné hrany.

Vypočítejte v cm³ objem pravidelného trojbokého hranolu. (Výsledek zaokrouhlete na dvě desetinná místa.)

Řešení

Objem pravidelného trojbokého hranolu je 93,53 cm³.

18. Obsahy trojúhelníků

Obsah pravoúhlého trojúhelníku KLM s pravým úhlem u vrcholu L je S = 60 cm² a jeho odvěsna |LM|=10 cm. Trojúhelníky KLM a RST jsou podobné, poměr podobnosti je k = 2,5.

Vypočítejte obsah trojúhelníku RST.

Řešení

Obsah trojúhelníku RST je 375 cm².

19. Obvod trojúhelníku

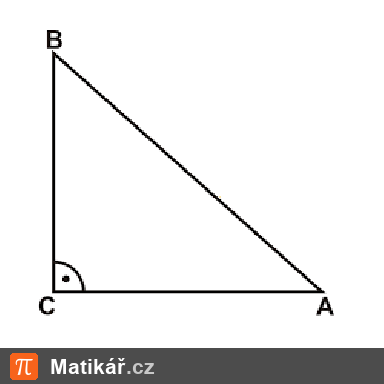
Vypočítej obvod trojúhelníku ABC, pokud víš, že je podobný trojúhelníku EFG, ve kterém |FG| = 144 mm, |EG| = 164 mm, |EF| = 92 mm a poměr podobnosti je 4.

Vypočítejte v cm obvod trojúhelníku ABC.

Řešení

Obvod trojúhelníku ABC je 160 cm.

20. Pochod z křižovatky

Na křižovatce dvou kolmých cest se rozdělila skupina turistů. Jedna skupina šla rychlostí 5,3 km/h. Druhá skupina 4,1 km/h.

Vypočtěte, kolik kilometrů byly od sebe obě skupiny vzdáleny po 1 h 25 min. (Zaokrouhlete na dvě desetinná místa.)

Řešení

Skupiny turistů byly od sebe vzdáleny 9,49 km.