Ve městě se plánuje oslavná událost, na kterou organizátoři připravili speciální světelné show. K dispozici mají 4 různé barvy světel: červenou, modrou, zelenou a žlutou. Každou barvu mohou použít vícekrát a pořadí barev při show je důležité.

Lucie má 5 různých knih, z nichž 2 určité knihy chtějí být vedle sebe na polici.

Evžen si stáhl 5 různých filmů ale má čas si pustit pouze 3, je jedno v jakém pořadí.

U hřiště stojí 10 mužů a 8 žen.

Na oslavě se sešlo 15 hostů. Při přípitku si každý s každým ťukl sklenicí právě jednou.


V obchodě je k dispozici 5 různých druhů ovoce: jablka, hrušky, meruňky, banány a kiwi.

Tomáš zapomněl čtyřmístný PIN, pamatuje si první tři čísla. Ví, že čtvrté číslo je liché.

Po skončení schůzky si všichni přítomní potřásli každý s každým rukou – celkem 105krát.

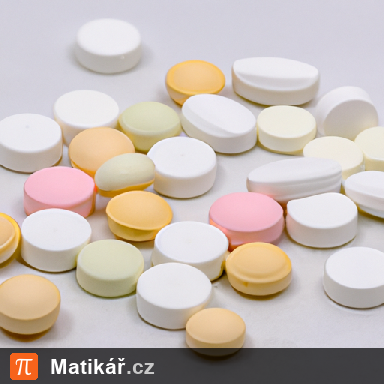
Podle klinických studií je účinnost léku 90 %. Lékař lék předepsal osmi pacientům.
Hodíme kostkou a pak hodíme tolikrát mincí, jaké číslo padlo na kostce.

Máme 15 červených a 5 bílých kuliček.

Jsou dané cifry 0, 1, 3, 4, 7.



Do taneční přišlo 32 chlapců a 34 dívek.

Z Ananasovic do Banánovic vede 5 cest, z Banánovic do Citrónovic vedou 3 cesty a z Citrónovic do Datlovic vedou 4 cesty.

V botníku jsou po jednom páru holínky, sandály, pantofle, hnědé a černé polobotky.


Ve městě Náhoda zrušily jízdní řády a autobusy MHD jezdí zcela náhodně. Představte si, že stojíte na zastávce, na které zastavuje 5 autobusů s čísly 12, 14, 15, 21 a 27 a vy se dvěma z nich můžete dostat domů.
